[Deep Learning: 신경망의 기초]다층퍼셉트론

9 minute read

다층 퍼셉트론

퍼셉트론 : 선형 분류기의 한계
- 선형 분리 불가능한 상황에서 일정한 양의 오류
- 예) XOR 문제에서 75% 정확도 한계
다층 퍼셉트론의 핵심 아이디어
- 은닉층을 둔다. 은닉층은 원래 특징 공간을 분류하는데 훨씬 유리한 새로운 특징 공간으로 변환한다.
- 시그모이드 활성함수를 도입한다. 연성에서는 출력이 연속값인데, 출력을 신뢰도로 간주함으로써 더 융통성 있게 의사결정을 할 수 있다. 0 아니면 1로 출력되는 계단함수가 아니라!
- 오류 역전파 알고리즘을 사용한다. 역방향으로 진행하면서 한번에 한 층씩 그레디언트를 게산하고 가중치를 갱신한다.

특징 공간 변환

퍼셉트론 2개를 사용한 XOR 문제의 해결
- XOR은 AND + OR이다. 이처럼 퍼셉트론 여러개의 조합을 통해 문제를 풀 수 있다. 즉 퍼셉트론을 여러개 사용한다.
퍼셉트론 2개를 병렬 결합하면,
- 원래 공간 x을 새로운 특징공간 z으로 변환 -> 새로운 특징 공간 z에서 선형 분리 가능함
- 퍼셉트론들의 조합에 의해 공간이 새롭게 바뀐다. 아무리 복잡하게 있는 공간이더라도 그 의미가 두드러지게끔 퍼셉트론의 선형, 비선형 요소를 사용해서 병렬적으로 배치한 은닉층을 통해 문제를 풀기 위한 유리한 공간으로 바꿀 수 있다.
추가 퍼셉트론 1개를 순차 결합하면,
- 새로운 특징 공간 z과 선형 분리를 수행하는 퍼셉트론을 순차 결합하면, 다층 퍼셉트론이 됨
- 해당 다층 퍼셉트론은 XOR 훈련집합에 있는 4개의 샘플을 제대로 분류한다.(0,0)(0,1)(1,0)(1,1) 이것은 단일 퍼셉트론으로는 xy좌표 4사분면 안에서 직선 하나로 구분할 수 없다!
원공간이 갖고있던 복잡성을 심플하게 만들고 주어져있는 정보의 손실이 없게끔 한다. 퍼셉트론이 가진 선형/비선형적인 연산에 의해 얻어질 수 있고, 그것들의 병렬배치를 통해 이뤄질 수 있다.
다층 퍼셉트론의 용량
- 3개의 퍼셉트론을 결합한 경우
  - 2차원 공간을 7개 영역으로 나누고 각 영역을 3차원 점으로 변환
  - 계단함수를 활성함수 $\tau$로 사용을 가정하였으므로 영역을 점으로 변환
- 일반화하여, p개 퍼셉트론을 결합하면 p차원 공간으로 변환

활성함수

딱딱한 공간 분할과 부드러운 공간 분할
- 계단함수는 딱딱한 의사결정(1 아니면 -1) -> 영역을 점으로 변환
- 그 외 활성함수는 부드러운 의사결정 -> 영역을 영역으로 변환
대표적인 비선형 함수인 S자 모양의 sigmoid를 활성함수로 사용
- 이진 시그모이드 함수, 양극 시그모이드 함수
- 활성 함수에 따른 다층 퍼셉트론의 공간 분할 능력 변화(+1과 -1로 나눠지는 부분, 즉 구간이 조정이 될 수 있다.)
신경망이 사용하는 다양한 활성함수
- logistic sigmoid와 tanh는 a가 커질수록 계단함수에 가까워짐
- 모두 1차 도함수 계산이 빠름(특히, ReLU는 비교 연산 한 번)
  - 활성함수로 사용되는 여러 함수
    - 계단함수 : 퍼셉트론(-1과1 사이로 매핑)
    - 로지스틱 시그모이드 : 이진 시그모이드, 다층 퍼셉트론(0과 1사이로 매핑)
    - 하이퍼볼릭 탄젠트 : 양극 시그모이드, 다층 퍼셉트론(-1과 1사이로 매핑)
    - 소프트플러스(0과 무한대 사이로 매핑)
    - 렉티파이어(ReLU) : 심층학습(0과 무한대 사이로 매핑)
- 활용 예
  - 퍼셉트론은 계단함수
  - 다층 퍼셉트론은 logistic sigmoid와 tanh
  - 심층학습은 ReLU
일반적으로 은닉층에서 logistic sigmoid를 활성 함수로 많이 사용(0~1사이 값으로 매핑시킴)
- S자 모양의 넓은 포화곡선*은 경사도 기반 학습(오류 역전파)을 어렵게 함 -> 깊은 신경망에서는 ReLU 활용.

구조

입력-은닉층-출력의 2층 구조의 경우
- d+1개의 입력 노드(d는 특징의 개수). c개의 출력 노드(c는 분류 개수)
- p개의 은닉 노드 : p는 하이퍼 매개변수(사용자가 정해주는 매개변수)
  - p가 너무 크면 과잉적합, 너무 작으면 과소적합 -> 5.5절의 하이퍼 매개변수 최적화
(2층 구조의 경우) 다층 퍼셉트론의 매개변수(가중치)
- 입력-은닉층을 연결하는 $U^1$
- 은닉층-출력을 연결하는 $U^2$
- 일반화하면 $u^1_{ji}$은 $l-1$번째 은닉층의 $i$번째 노드를 $l$번째 은닉층의 $j$번째 노드와 연결하는 가중치
  - 입력을 0번째 은닉층, 출력을 마지막 은닉층으로 간주

동작

특징벡터 x를 출력벡터 o로 사상(mapping)하는 함수로 간주할 수 있음
- 예 : 2층 퍼셉트론 : $o = f(x) = f_2(f_1(x))$
- 깊은신경망은 층, 즉 레이어가 4개 이상인 것
노드가 수행하는 연산을 구체적으로 쓰면,
- j번째 은닉 노드의 연산 : $z_j = \tau(zsum_j)$, $zsum_j = u_j^1x$
  - $u_j^1$은 j번째 은닉 노드에 연결된 가중치 벡터
- k번째 출력 노드의 연산 : $o_k = \tau(osum_k)$, $osum_k = u_k^2z$
  - $u_k^2$는 k번째 출력 노드에 연결된 가중치 벡터
다층 퍼셉트론의 동작을 행렬로 표기하면, $o = \tau(U^2\tau_h(U^1x))$
은닉층은 특징 추출기
- 은닉층은 특징 벡터를 분류에 더 유리한 새로운 특징 공간으로 변환
- 현대 기계학습에서는 특징학습이라 부름(심층학습은 더 많은 층을 거쳐 계층화 된 특징학습을 함)

구조

기본 구조
- 범용적 근사 이론
  - 하나의 은닉층은 함수의 근사를 표현 -> 다층 퍼셉트론도 공간을 변환하는 근사 함수
- 얕은 은닉층의 구조
  - 지수적으로 더 넓은 폭이 필요할 수 있음
  - 더 과잉적합 되기 쉬움
- 일반적으로 얕고 넓은 폭의 은닉층 구조보다 깊은 은닉층의 구조가 좋은 성능을 가짐
은닉층의 깊이에 따른 이점
- 지수의 표현
  - 원공간이 종이 한장이라고 생각했을 때, 이 종이를 접고 접어서 원공간에서는 직선으로 분류할 수 없는 것을 종이를 여러번 접음에 따라(은닉층이 깊어짐에 따라) 선형으로 간단하게 분류할 수 있다.
  - 각 은닉층은 입력 공간을 어디서 접을지 지정 -> 지수적으로 많은 선형적인 영역 조각들
- 성능 향상

다층 퍼셉트론에 의한 인식

다층 퍼셉트론 학습 과정
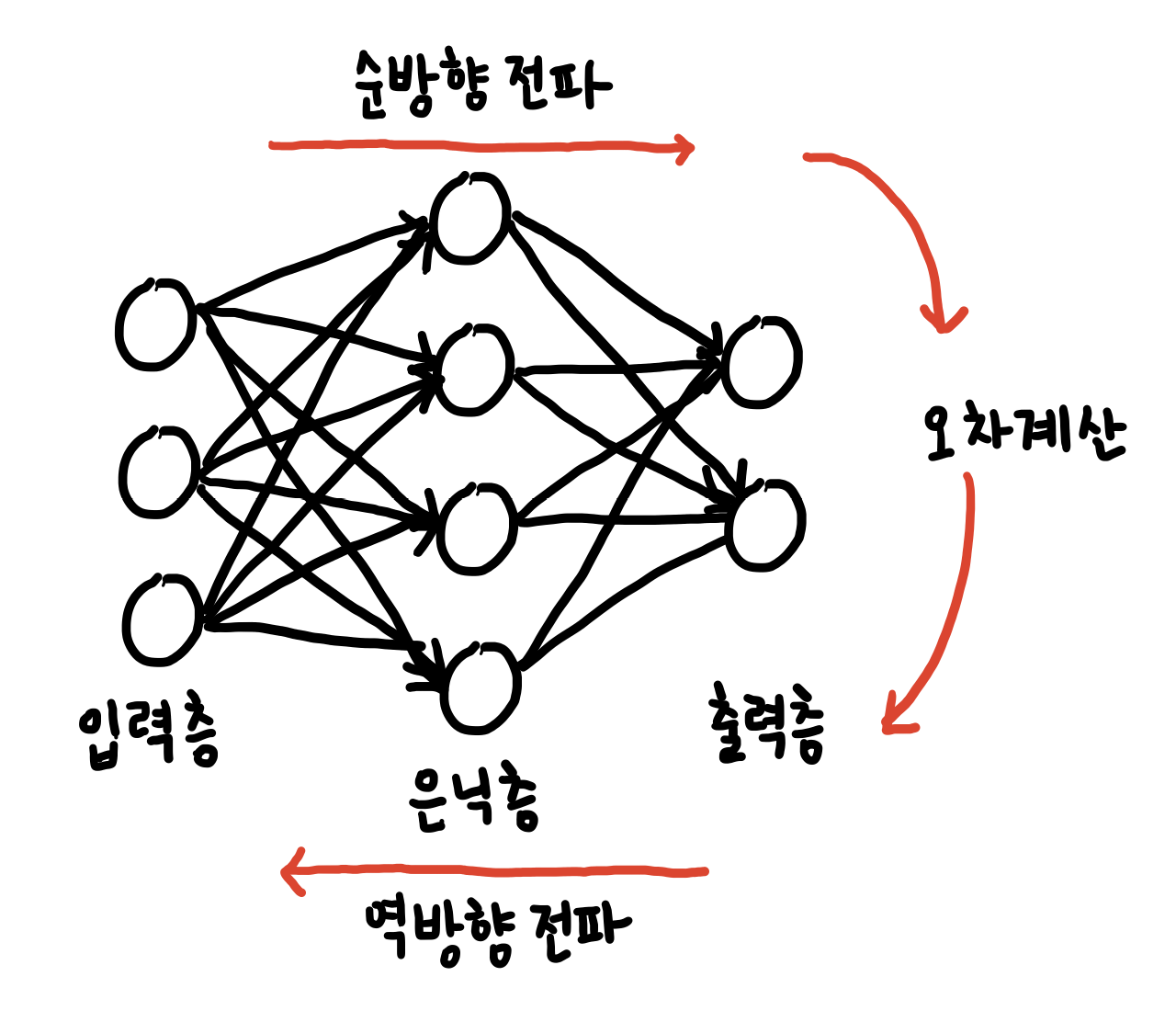
예측 단계
- 학습을 마친 후 현장 설치하여 사용(또는 테스트 집합으로 성능 테스트)
- 입력 : 테스트 샘플 x
- 출력 : 부류 y
- 전방 계산 한번만 사용하므로 빠름
다층 퍼셉트론 시각화 : https://playground.tensorflow.org

오류 역전파 알고리즘의 빠른 속도

연산 복잡도 비교
- 오류 역전파 : 전방 계산 대비 약 1.5~2배의 시간 소요 <- 비교적 빠름(연쇄법칙)
  - c: 분류 수, d: 특징 차원, p: 은닉층 차원
- 학습 알고리즘은 오류 역전파 반복하여 점근적 시간복잡도는 $\Theta((cp+dp)np)$
  - n: 훈련집합의 크기, q: epoch 수

모든 함수를 정확하게 근사할 수 있는 능력

은닉 노드가 충분히 많다면, 활성함수로 무엇을 사용하든 표준 다층 퍼셉트론은 어떤 함수라도 원하는 정확도만큼 근사화할 수 있다.

성능 향상을 위한 경험의 중요성

순수한 최적화 알고리즘으로는 높은 성능 불가능
- 데이터 희소성, 잡음, 미숙한 신경망 구조 등 때문에!
- 성능 향상을 위한 다양한 경험을 개발하고 공유해야함.
신경망의 경험적 개발에서 주요 쟁점
- 아키텍처 : 은닉층과 은닉 노드의 개수 정하기
- 초깃값 : 가중치 초기화할때 난수이지만 그 값의 범위와 분포가 중요
- 학습률 : 처음에는 큰 값->점점 줄이기
- 활성함수 : 초창기 다층 퍼셉트론은 로지스틱 시그모이드 -> 깊은 신경망에서는 주로 ReLU사용

오류 역전파 알고리즘

png
순방향 전파로 w_1, w_2를 통해서 나온 예측값과 실제값의 차이를 줄이기 위해 각각의 w_1, w_2를 경사하강법을 취해 목적함수 J(w)를 가중치로 편미분하여 최소화한다.
즉 w_2에서 들어오는 오차가 w_1에 영향을 미치게 되는데 이게 back propagation이다.
역전파 방법은 결과 값을 통해서 다시 역으로 input 방향으로 오차를 다시 보내며 가중치를 재업데이트 하는 것이다. 물론 결과에 영향을 많이 미친 노드(뉴런)에 더 많은 오차를 돌려줄 것이다.

목적함수의 정의

훈련집합
- 특징 벡터 집합 $X$, $Y$
- 분류 벡터는 one-hot코드로 표현됨. 즉 $y_i = (0,0,…,1,…,0)^T$
기계학습의 목표
- 모든 샘플을 옳게 분류하는 함수 f를 찾는 일
목적함수
- 가장 많이 쓰이는 평균 제곱 오차(MSE)
  - L2 norm 사용
  - 온라인 모드 : 배치모드를 스트리밍으로 하는 것.
  - 배치 모드 : 데이터셋을 특정 단위 n개만큼 보는 것.

오류 역전파를 이용한 학습 알고리즘

연산그래프(전방 연산을 그래프로 표현할 수 있음)
연쇄 법칙(chain rule)의 구현
- 반복되는 부분식들을 저장하거나 재연산을 최소화(예: 동적 프로그래밍)
- 그래디언트를 구할 때 신경망에서 연속해서 일어나는 연쇄법칙을 오류역전파할때 활용한다.
- ${\partial E \above 1pt \partial w_{ij}} = {\partial E \above 1pt \partial o_j}{\partial o_j \above 1pt \partial net_j}{\partial net_j \above 1pt \partial w_ij}$
- 체인룰(연쇄법칙)을 통해 끝에서부터 나오는 오류(손실함수)를 내가 원하는 위치까지 보낼 수 있다.
목적함수를 다시 쓰면, $J(\Theta) = {1 \above 1pt 2}\left | y - o(\Theta) \right |_{2}^{2}$(2층 퍼셉트론의 경우 $\Theta = {U^1, U^2}$)
이 목적함수의 최저점을 찾아주는 경사하강법(2층 퍼셉트론의 경우)
- $U^1 = U^1 - \rho {\partial J \above 1pt \partial U^1}$
- U^2 = U^2 - \rho {\partial J \above 1pt \partial U^2}
- $X -> U^1_ -> U^2 -> J(\Theta)$으로 연산이 순차적으로 진행된다.
- 이걸 역으로 미분하여 체인룰을 통해 오류역전파를 사용하여 내가 원하는 위치의 것을 활용할 수 있다.
오류 역전파 알고리즘
- 출력의 오류를 역방향(오른쪽에서 왼쪽으로)으로 전파하며 경사도를 계산하는 알고리즘
- 반복되는 부분식들의 경사도의 지수적 폭발(exponential explosion) 혹은 사라짐(vanishing)을 피해야함.
[경사도 단순화] 역전파 분해(backprop with scalars) x, y, z가 서로 스칼라라고 하자. 두 입력이 들어와서 처리를 해서 내보내는 것을 생각해보자.

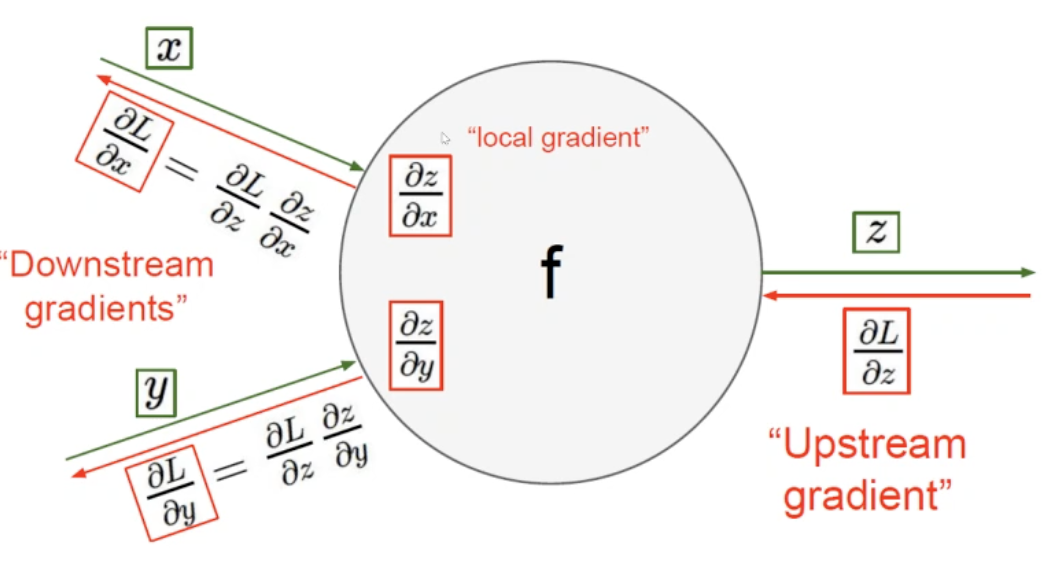
L은 loss(z-실제값),이것을 내가 원하는 위치(가중치)의 미분을 구한다. z에서 구하고 싶으면 L을 z에 대해 미분하고, x에서 구하고 싶으면 L을 z에 대해 미분한 것 * z를 x에 대해 미분한 것(체인룰!) Downstream gradient는 연산을 통과시키기 이전에 있었던 값이다.
단일 노드역전파
- in -> f(함수) -> out 의 forward구조일 때
- ${\partial \varepsilon \above 1pt \partial in} = {\partial \varepsilon \above 1pt \partial out}\cdot {\partial out \above 1pt \partial in} = {\partial \varepsilon \above 1pt \partial out}\cdot f’(in)$
덧셈의 역전파의 예
- in 여러개 -> $\Sum$ -> out의 forward 구조일 때
- ${\partial \varepsilon \above 1pt \partial in} = {\partial \varepsilon \above 1pt \partial out}\cdot {\partial out \above 1pt \partial in} = {\partial \varepsilon \above 1pt \partial out}\cdot 1$
S자 모양 활성함수의 역전파 예
- in -> 활성함수 -> out의 forward 구조일 때
- ${\partial \varepsilon \above 1pt \partial in} = {\partial \varepsilon \above 1pt \partial out}\cdot {\partial out \above 1pt \partial in} = {\partial \varepsilon \above 1pt \partial out}\cdot \sigma’(in) = {\partial \varepsilon \above 1pt \partial out}\cdot [\sigma(in)(1-\sigma(in))]$
최대화의 역전파 예
- ${\partial \varepsilon \above 1pt \partial in} = {\partial \varepsilon \above 1pt \partial out}\cdot {\partial out \above 1pt \partial in}$
- 결과
  - ${\partial \varepsilon \above 1pt \partial out}$(if in_i is max)
  - 0(otherwise)
fanout(forward) <=> sum(backprop)
도함수의 종류
- Scalar to Scalar : regular derivative
- Vector to Scalar(편미분) : Derivative is Gradient
- Vector to Vector : Derivative is Jacobian
오류 역전파 미분의 연쇄 법칙이용
- 연쇄 법칙
  - 스칼라인 경우, ${dz \above 1pt dx} = {dz \above 1pt dy}{dy \above 1pt dx}$
  - 벡터인 경우, $\bigtriangledown_x^z = ({\partial y \above 1pt \partial x})^T \triangledown_y^z$
    - x가 m차원 -> y가 n차원 -> 결과가 스칼라 인 경우로 forward인 구조인 경우!
    - 야코비안 행렬과 경사도를 곱한 연쇄 법칙을 얻어서 구함. (야코비안과 그래디언트의 곱)
행렬 표기 : GPU를 사용한 고속 행렬 연산에 적합. 스칼라, 벡터보다 행렬이 좋다! GPU 연산을 할 수 있게끔 미니배치로 행렬을 만든다.

미니배치 확률론적 경사 하강법

미니배치 방식
- 미니배치(텐서 버전)
- 한번에 t개의 샘플을 처리(t = 미니배치 크기)
  - t=1이면 확률론적 경사 하강법
  - t=n(전체)이면 배치 경사 하강법
- 경사도의 잡음을 줄여주는 효과 때문에 수렴이 빨라짐
- GPU를 사용한 병렬처리에도 유리함
- 현대 기계 학습은 미니배치 기반의 확률론적 경사 하강법을 표준처럼 여겨 널리 사용함.

실습

Pytorch Tutorial - Autograd & MLP(Multi-layer perceptron)

Autograd

autograd 패키지는 텐서의 모든 연산에 대한 자동 미분을 제공
실행-기반-정의(define-by-run) 프레임워크로, 코드를 어떻게 작성하여 실행하느냐에 따라 역전파가 정의된다는 것을 의미
역전파는 학습 과정의 매 단계마다 달라짐

Tensor

torch, Tensor 클래스의 .requires_grad 속성을 True로 설정하면, 해당 텐서에서 이루어진 모든 연산을 추적(track)하기 시작
계산이 완료된 후, backward()를 호출하여 모든 변화도(gradient)를 자동으로 계산할 수 있으며 이 Tensor의 변화도는 .grad 속성에 누적됨
Tensor가 기록을 추적하는 것을 중단하게 하려면, .detach()를 호출하여 연산기록으로부터 분리하여 연산이 추적되는 것을 방지할 수 있음
기록을 추적하는 것(과 메모리를 사용하는 것)을 방지하기 위해서 코드 블럭을 with torch.no_grad():로 감쌀 수 있음
이는 변화도(gradient)는 필요 없지만 requires_grad=True가 설정되어 학습 가능한 매개변수를 갖는 모델을 평가(evaluate)할 때 유용
Autograd 구현에서 Function 클래스는 매우 중요한 역할을 수행
Tensor와 Function은 서로 연결되어 있고 모든 연산 과정을 부호화하여 순환하지 않는 그래프를 생성
각 tensor는 .grad_fn 속성을 가지고 있는데 이는 Tensor를 생성한 Function을 참조함(단, 사용자가 만든 Tensor는 예외이며, 사용자가 만든 Tensor가 아닌 연산에 의해 생긴 텐서와 같은 경우는 모두 Function을 참조)
도함수를 계산하기 위해서는 Tensor의 .backward()를 호출하면 됨

ANN(Artificial Nequral Networks)

신경망은 torch.nn 패키지를 사용하여 생성할 수 있음
nn은 모델ㅇ르 정의하고 미분하기 위해서 위에서 살펴본 autograd를 사용
nn.Module은 계층(layer)과 output을 반환하는 forward(input) 메소드를 포함
간단한 순전파 네트워크(feed-forward-network)
입력을 받아 여러 계층에 차례로 전달한 후, 최종 출력을 제공
신경망의 일반적인 학습 과정
- 학습 가능한 매개변수(가중치)를 갖는 신경망을 정의
- 데이터 셋 입력을 반복
- 입력을 신경망에서 전파(프로세스)
- 손실(loss; 입력 값과 예측 값과의 차이)를 계산
- 변화도(gradient)를 신경망의 매개변수들에 역으로 전파 - 역전파 과정
- 신경망의 가중치를 갱신
  - 새로운 가중치(weight) = 가중치(weight) - 학습률(learning rate) * 변화도(gradient)

손실함수(Loss Function)

손실함수는 (output, target)을 한 쌍으로 입력받아, 출력이 정답으로부터 얼마나 떨어져 있는지 추정하는 값을 계산
forward 함수만 정의하고 나면 backward함수는 autograd를 사용하여 자동으로 정의됨
모델의 학습 가능한 매개 변수는 net.parameters()에 의해 변환됨

가중치 갱신

가장 단순한 갱신 규칙은 확률적 경사하강법(SGD)
새로운 가중치(weight) = 가중치(weight) - 학습률(learning rate) * 변화도(gradient)

TensorFlow Tutorial

자동 미분과 그래디언트 테이프

그레디언트 테이프

텐서플로는 자동미분을 위한 tf.GradientTape API를 제공
tf.GradientTape는 컨텍스트 안에서 실행된 모든 연산을 테이프에 ‘기록’
후진 방식 자동 미분(reverse mode differetiation)을 사용해서 테이프에 ‘기록된’ 연산 그래디언트를 계산

제어 흐름 기록

연산이 실행되는 순서대로 테이프에 기록되기 때문에, 파이썬 제어흐름이 자연스럽게 처리됨
연산이 파이썬과 동일한 순서대로 돌아간다.

고계도(Highter-order) 그래디언트

GradientTape 컨텍스트 메이저 안에 있는 연산들은 자동미분을 위해 기록됨
만약 이 컨텍스트 안에서 그래디언트를 계산하면 해당 그래디언트 연산 또한 기록됨

ANN

Sequencial 모델을 사용하는 경우

Sequencial 모델은 각 레이어에 정확히 하나의 입력 텐서와 하나의 출력 텐서가 있는 일반 레이어 스택에 적합

오늘 한 부분 어려웠다! 이론 강의 부분 시간날때 한번 더 보기!

Twitter Facebook LinkedIn

채린