[인공지능 수학 - 자료의 정리]7강 : 벡터와 직교분해
벡터와 직교분해
벡터의 표현
n-벡터는 크기와 방향을 가진 물리량으로 다음과 같이 표현될 수 있다.
좌표게 없이 표현
- v : 화살표로 표현
- v의 크기 : 화살표의 길이 측정
- v의 방향 : 화살표의 방향 측정
좌표계를 도입하여 표현
- $v = (v_1, v_2, \dots, v_n)$
- v의 크기 : $|v| = \sqrt{v^2_1 + v^2_2 + \dots + v^2_n}$
- v의 방향 : $1/|v|v$
벡터의 내적
두 벡터 u와 v에 대한 내적(inner product 혹은 dop product)는 다음과 같이 정의된다.
좌표게 없이 표현
두 n-벡터의 길이와 두 벡터 간의 사이각 $\theta$을 통해 다음과 같이 정의된다.
$u \cdot v = |u||v|cos\theta$
좌표계를 도입하여 표현
$u = (u_1, u_2, \dots, u_n)$, $v = (v_1, v_2, \dots, v_n)$의 좌표값을 통해 다음과 같이 계산된다.
$u \cdot v = (u_1v_1, u_2v_2, \dots, u_nv_n)$
어떤 식으로든, 두 벡터의 내적은 숫자가 나오게 돼있다.
두 벡터 u, v간의 내적이 0이면 두 벡터는 직교(orthogonal)이다.
$u\cdot v = 0 \Leftrightarrow u \perp v$
직교의 물리적 의미
벡터 u, v가 직교일 때, u방향으로의 전진은 v 방향에서 전혀 측정되지 않는다. 그 반대도 마찬가지이다. 즉 따로따로 측정해도 무방하다. (고교 과정에서 배운 xy-좌표계나 xyz-좌표계와 같은 데카르트 좌표계가 직교좌표계였음을 상기하도록 하자.)
투영(projection)
두 벡터 u, a가 있을 때, 벡터 u를 a 위에 투영한 벡터(u벡터를 a벡터에 수선의 발을 내리는 것)를 $proj_au$라 하고 다음과 같이 구한다.
$proj_au = (u \cdot {1 \above 1pt \left | a \right |}\left | a \right |)({1 \above 1pt \left | a \right |}\left | a \right |) = ({u \cdot a \above 1pt \left | a \right |^2})a$
= (길이)*(방향) = (기저 a에 대한 좌표값)a
벡터 u를 a 위에 투영하고 남은 보완 벡터(complement vector)는 $u-proj_au$이다.
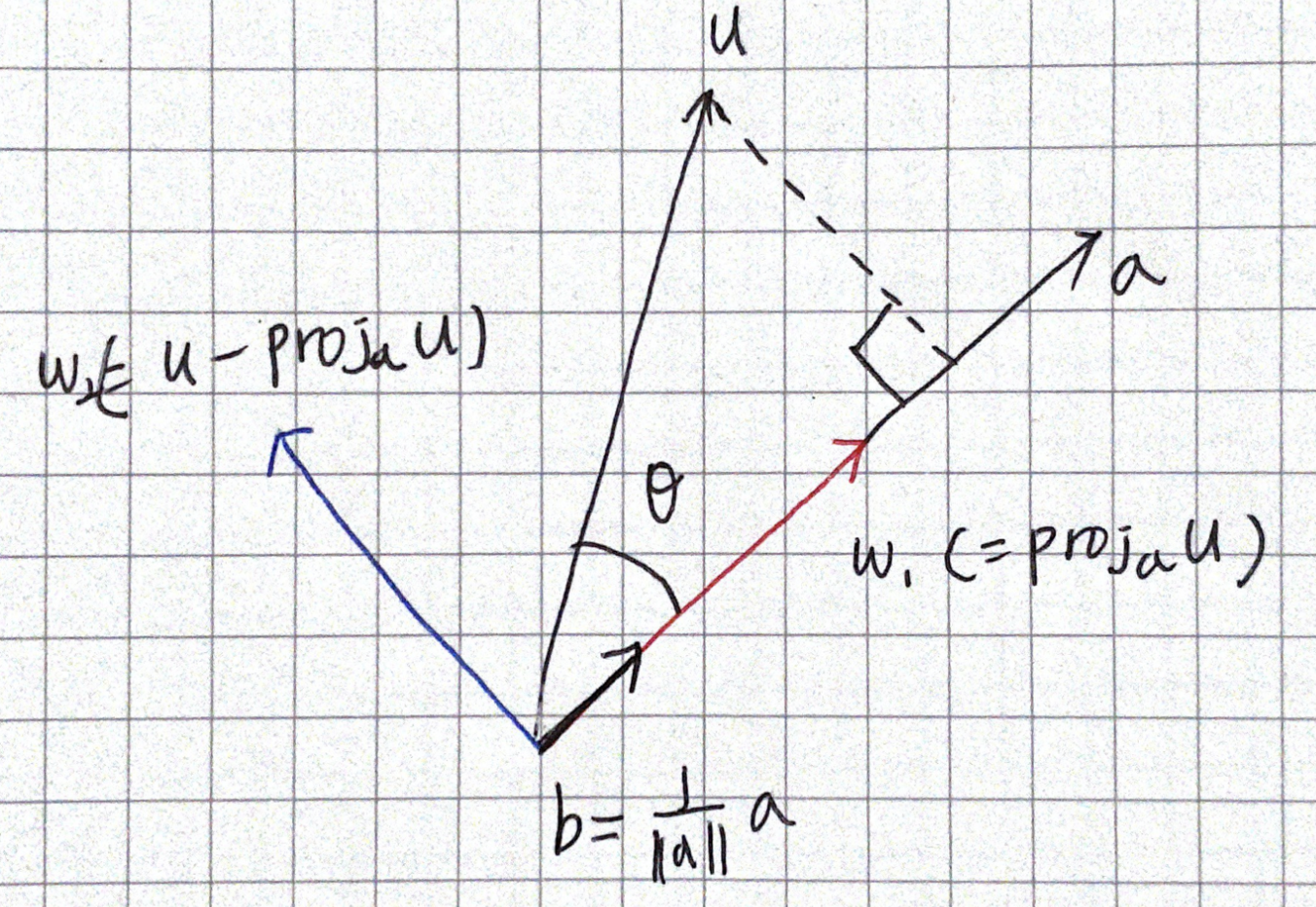
투영(projection)과 남은 보완(complement)벡터의 그림, 투영과 보완은 직교한다.

투영과 보완벡터는 직교한다는 사실이 중요!
두 벡터 u, a가 있을 때, 투영과 보완의 개념을 이용해 직교분할할 수 있다.
$proj_au \perp (u - proj_au)$
$u = proj_au + (u - proj_au)$
직교행렬(Orthogonal Matrix): 직교좌표계에 대한 행렬 표현
직교행렬(Orthogonal Matrix)
행렬은 좌표계라는 의미를 이미 배웠다. 즉, 행렬은 각 열벡터가 기저(basis)를 이루는 좌표계(coordinate system)이다.
직교행렬(orthogonal matrix)
주어진 행렬의 모든 열벡터가 서로 직교한다면, 이 행렬을 직교행렬이라 한다. 직교행렬은 직교좌표계를 의미한다.
직교행렬은 $QQ^{-1} = Q{-1}Q = I$을 만족한다.
$
\begin{bmatrix}
1 & 4\cr
-2 & 2\cr
\end{bmatrix}
$
$
\begin{bmatrix}
2 & 2 & -4\cr
2 & 1 & 7\cr
6 & -1 & -1\cr
\end{bmatrix}
$
정규직교행렬(orthogonal normal matrix)
주어진 행렬이 직교행렬이고 모든 열벡터의 크기가 1이라면 이 행렬을 정규직교행이라 한다. 정규직교행렬은 정규직교좌표계를 의미한다.
$
\begin{bmatrix}
1 \over \sqrt 5 & 2 \over \sqrt 5\cr
-2 \over \sqrt 5 & 1 \over \sqrt 5\cr
\end{bmatrix}
$
$
\begin{bmatrix}
1 \over \sqrt 11 & 2 \over \sqrt 6 & -4 \over \sqrt 66\cr
1 \over \sqrt 11 & 1 \over \sqrt 6 & 7 \over \sqrt 66\cr
3 \over \sqrt 11 & -1 \over \sqrt 6 & -1 \over \sqrt 66\cr
\end{bmatrix}
$
직교행렬을 정규직교행렬로 만든 것이다. 열방향으로 원소들을 더해보면 1이 됨을 알 수 있다.
직교행렬(Orthogonal Matrix)을 이용한 선형시스템
선형시스템 $Ax = b$에서 행렬 A가 직교행렬(orthogonal matrix)이면, 해(solution) x는 역행렬 $A^{-1}$의 계산 없이 다음과 같이 구할 수 있다.
- x의 i-번째 요소는 투영(projection)으로 계산할 수 있다. 즉, 벡터 b를 행렬 A의 각 열벡터 $a_i$에 투영한 연산 $proj_{a_i}b$로부터 $x_i = b \cdot a_i \over |a_i|^2$임을 계산할 수 있다.
- x의 i-번째 요소와 j-번째 요소의 계산은 독립적이다. 즉, x의 계산은 병렬처리 가능하다.
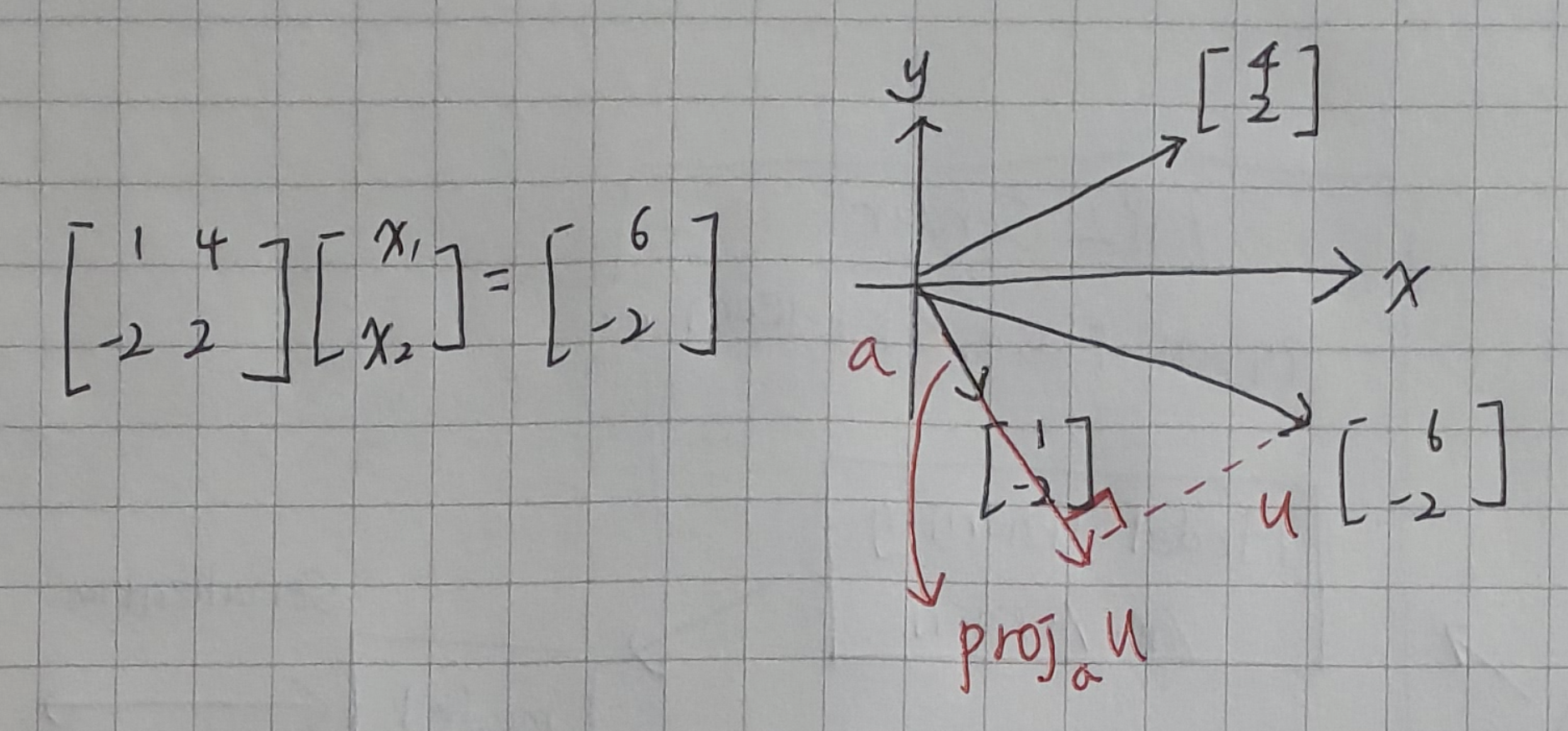
왼쪽의 행렬식에서 x1=2, x2=1임을 쉽게 알 수 있다. 직교하기 때문에 직관적으로 각 방향으로 몇번 이동해야 되는지 알기 쉽다. 역행렬을 계산하지 않고 투영(각각의 축에 수선의 발을 내리기)을 통해 병렬처리하여 계산할 수 있다는 것이 핵심!
정규직교행렬(Orthonormal Matrix)을 이용한 선형시스템
선형시스템 $Ax = b$에서 행렬 A가 정규직교행렬(orthonormal matrix)이면, 해(solution)는 역행렬 $A^{-1}$의 계산 없이 다음과 같이 구할 수 있다.
- x의 i-번째 요소는 내적(inner product)으로 계산할 수 있다. 즉, 벡터 b를 행렬 A의 각 열벡터 $a_i$에 투영한 연산 $proj_{a_i}b$로부터 $x_i = b \cdot a_i$임을 계산할 수 있다.
- x의 i-번째 요소와 j-번째 요소의 계산은 독립적이다. 즉, x의 계산은 병렬처리 가능하다.
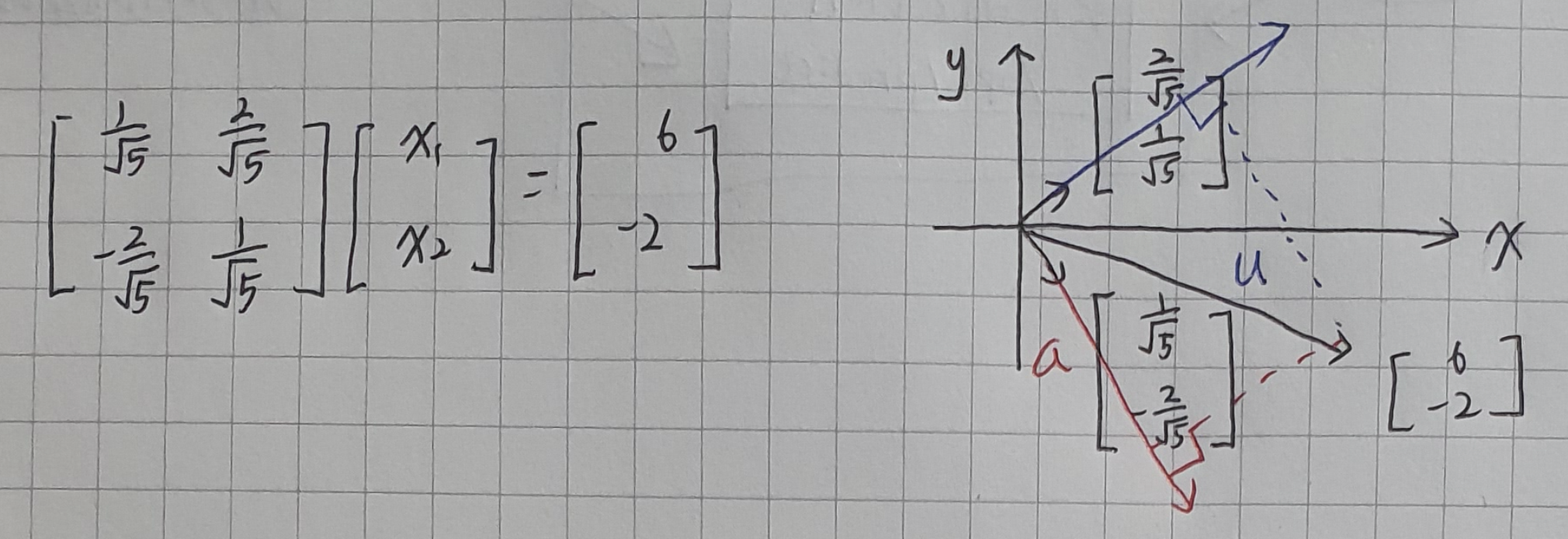
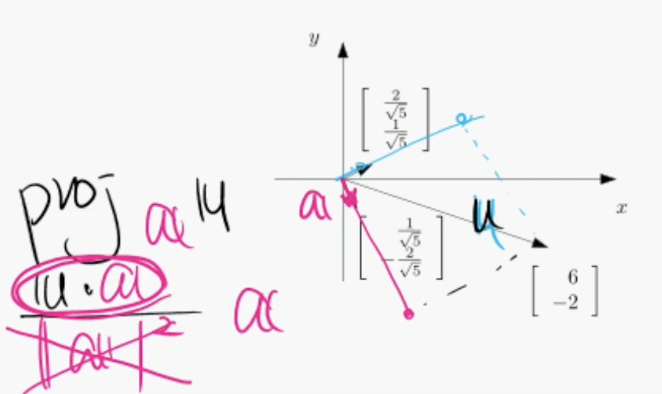
정규직교행렬은 역행렬도, 투영도 필요없고 내적만으로도 계산 가능!
QR 분해: A = QR 주어진 행렬에서 정규직교행렬 추출
행렬분해(matrix decomposition)의 의미
주어진 행렬을 행렬분해된 상태로 가지고 있으면 여러모로 계산이 편한 경우가 많다. 다음은 대표적인 행렬분해이다.
- LU 분해(LU decomposition)
- QR 분해(QR decomposition)
- 특이값 분해(SVD, Singular Value Decomposition) QR 분해는 직교분할과 관련이 있습니다.
QR decomposition(QR 분해)
QR 분해는 주어진 행렬을 아래의 형태를 가지는 두 행렬의 곱으로 나누는 행렬분해이다.
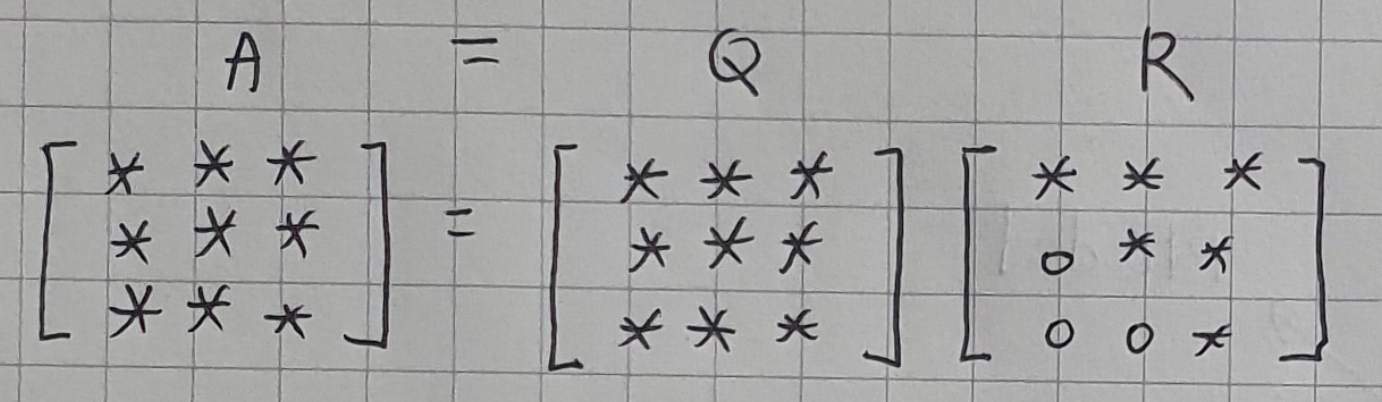
- Q : orthonormal matrix(정규직교행렬)
- U : upper triangular matrix(상삼각행렬), 직교성분을 빼낸 찌꺼기 성분. back substrition의 장점을 누릴 수 있다.
주어진 행렬 A가 QR분해되어 있을 때의 장점
QR 분해를 이용해 $Ax = b$ 문제를 아래와 같이 나타내면
$Ax = b$ -> $(QR)x = b$ -> $Q(Rx) = b$ -> $Qy = b$, (단, $Rx = y$)
선형시스템을 다음과 같이 두 단계로 간단히 해결할 수 있음을 알 수 있다.
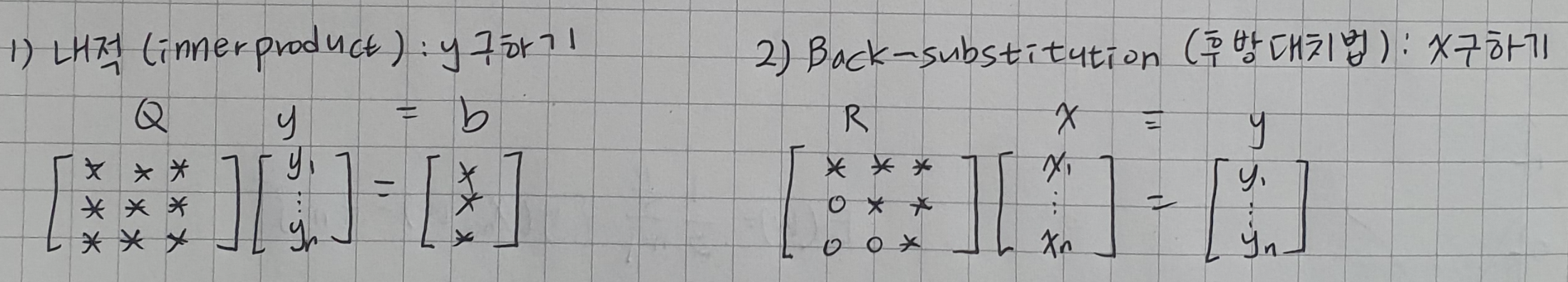
y는 내적으로 풀 수 있게 된다. Q의 첫번째 칼럼과 b를 내적하면 y1, Q의 n번째 칼럼과 b를 내적하면 yn이 나오게 된다.
R이 상삼각행렬이므로 후방대치법을 통해 x를 편하게 구할 수 있다.
QR decomposition(QR 분해)의 의미
QR 분해는 그람-슈미트 과정(Gram-Schmidt process)을 행렬로 코드화 한 것이다.
- Q : 행렬 A에서 정규직교성을 추출한 행렬
- R : 행렬 A에서 정규직교성 추출 후 남은(residual), upper triangular matrix(상삼각행렬) QR분해는 주어진 행렬에서 정규직교성을 추출하여 계산의 편의를 도모한다.
QR decomposition(QR 분해)의 활용
- 빠른 계산 : 선형시스템 $Ax = b$의 해를 구할 때, 정규직교행렬(orthonormal matrix) Q를 이용한 계산 부분은 병렬처리로 빨리 계산할 수 있다. 그러나 R을 이용한 계산 부분은 병렬처리 할 수 없다.
- b가 자주 업데이트 되는 경우 : 선형시스템 $Ax = b$에서 행렬 A는 고정되어 있고 b가 자주 변하는 문제가 종종 있다. 이런 경우, 행렬 A를 미리 QR로 분해해 둔다면, b가 업데이트될 때마다 선형시스템의 해 x를 실시간으로 구할 수 있다.
QR 분해 vs LU분해
- LU분해의 경우, 선형시스템을 풀 때 병렬처리 할 수 없다
- QR분해의 경우, Q 행렬이 꽉 찬 구조를 가진 행렬이므로 메모리 사용량이 많다. LU분해는 L, U파트 각각 수가 절반씩만 차 있다.
