모평균의 추정Permalink

• 표본 평균의 특성
  • 표본 평균(sample mean) 사용
  • $\bar {X}$는 모평균 $\mu$의 추정에 사용되는 통계량
• 대표본인 경우
  • 중심극한 정리에 의해 표본평균이 정규분포를 따른다고 가정함

점추정Permalink

• 표본평균이 점 추정값(추정량)이 됨(모평균의 점 추정값은 표본평균이다.)

•   import numpy as np
    samples = [9,4,0,8,1,3,7,8,4,2]
    print(np.means(sample))
  

  점추정만 가지고는 확률적인 근거를 제공하기 부족하기 때문에, 구간추정이라는 것을 이용한다.

구간추정Permalink

• 모평균 $\mu$의 $100(1 - \alpha)%$ 신뢰구간(confidence interval) : 표본을 뽑았을 때 그걸 100번을 반복하면 alpha 만큼은 제기산 구간(아래 사진) 안에 모평균이 존재할 것이다 라는 의미!
  • ($\mu$의 추정량) \pm $z_{a/2} (추정량의 표준편차)$
• 따라서 정규분포에서 $\sigma$를 알 때, 신뢰구간은 다음과 같다.
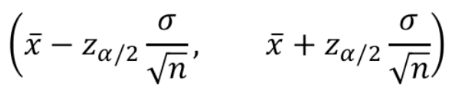
• 실용적이지 못함 : 정규분포가 아니거나 표준편차가 알려져 있지 않음. 따라서 일반적으로 이 수식으로 신뢰구간을 구하진 않는다.
  
  

모집단이 정규분포가 아니고 표본의 크기가 작으면 중심극한 정리를 사용하지 못한다. 하지만…

• 표본의 크기가 클 때 중심극한 정리 사용
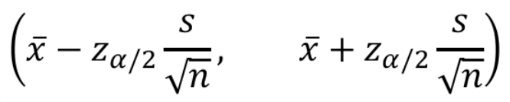
  • ($\mu$의 추정량) \pm $z_{a/2} (추정량의 표준편차)$

• $s$ : 표본표준편차 모양은 거의 비슷한데 시그마가 s로 바뀜.
  
  
  

• 어떤 학교의 고1남학생의 평균키를 추정하기 위해 36명을 표본으로 추출하여 그 표본평균과 표본표준편차를 계산하여 그 결과가 아래와 같다.
• $\bar {x} = 173.6, s = 3.6$
• 평균키에 대한 95% 신뢰 구간을 구하시오.
  • 95%의 신뢰도이므로 양 귀퉁이가 5%에 해당하게 된다. (정규분포 그래프에서) 따라서 $\alpha = 0.05$가 되므로, 문제에서 주어진 표본평균과 표본표준편차도 대입하면 (172.4, 174.8)의 구간이 나온다.
    
    
• 평균 구하는 방법

  xbar = np.mean(리스트)
  

• 표준편차 구하는 방법

  sd = np.std(리스트, ddof=1)
  

  
  
  
  

모비율의 추정Permalink

점추정Permalink

• 확률변수 X :
  • n개의 표본에서 특정 속성을 갖는 표본의 개수
• 모비율 $p$의 점추정량
  • $\hat{p} = {X \above 1pt n}$ 점추정보다는 구간추정을 더 많이 사용한다.
    
    
    

구간추정Permalink

• n이 충분히 클 때($n \hat{p}$ > 5, $n(1 - \hat{p})$ > 5일 때를 의미)
  • $X$ ~ $N(np, np(1-p))$ : 확률변수 X가 정규분포를 따른다.
• 확률변수 X의 표준화
  • 
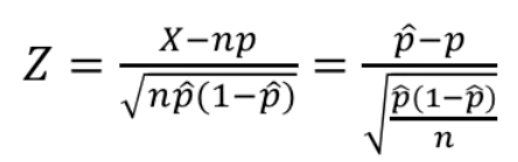
  • 근사적으로 표준정규분포 $N(0,1)$를 따름

• $P(

  Z

  \leq z_{a/2}) = 1 - \alpha$

• 모비율 $p$의 $100(1 - \alpha)%$ 신뢰구간(confidence interval), 이 구간 안에 $p$가 있을 확률이 $1 - \alpha$
  • 
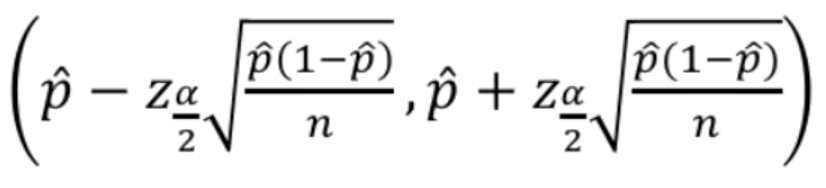
    파이썬으로 코드를 짜면 다음과 같다.

    import numpy as np
    x=48
    n=150
    phat = x/n
    alpha = 0.05
    zalpha = scipy.stats.norm.ppf(1-alpha/2)
    sd = np.sqrt(phat*(1-phat)/n)
    print("phat %.3f, zalpha: %.3f, sd: %.3f"%(phat, zalpha, sd))
    ci = [phat - zalpha * sd, phat + zalpha * sd]
    print(ci)