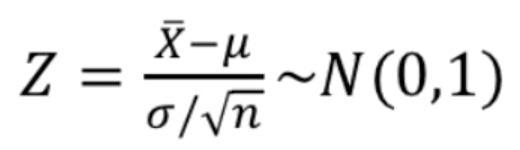[인공지능 수학 - 통계학]17강 : 검정
통계적 가설검정
가설검정
- 예)
- 어떤 고등학교의 1학년 학생들의 평균키가 170.5cm으로 알려져 있었다. 올해 새로 들어온 1학년 학생들 중 30명을 랜덤하게 선택하여 키를 잰 후 평균을 계산했더니 171.3cm이었다.
- 올해 신입생은 평균키가 170.5cm보다 더 크다고 할 수 있는가?
- 이러한 주장을 검증하는 것이 가설 검정임
- 표본평균 $\bar {X}$가 $\mu_0$보다 얼마나 커야 모평균 $\mu$가 $\mu_0$보다 크다고 할 수 있을 것인가?
- 표본평균은 표본의 선택에 의해 달라짐을 주의
- 표본평균은 표본의 선택에 의해 달라짐을 주의
- 귀무가설 $H_0 : \mu = \mu_0$
- 대립가설 $H_1 : \mu > \mu_0$
- 귀무가설을 기각하기 위해서는 $\bar {X}$(표본평균)가 좀 큰 값이 나와야 함.
- 귀무가설이 참이라고 가정할 때, 랜덤하게 선택한 표본에서 지금의 $\bar {X}$가 나올 확률을 계산할 필요
- 이 확률이 낮다면 귀무가설이 참이 아니라고 판단
- 확률이 낮다는 기준점 필요
- 유의수준 $\alpha$ 도입
- $P(\bar {X} \geq k) \leq \alpha$가 되는 k를 찾아야 함
- 표준정규확률변수로 변환 -> 검정통계량이라고 함
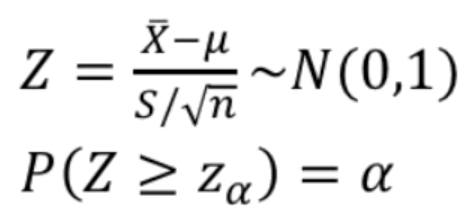
- 표준정규분포를 따른다.
- 따라서 $\bar {X}$를 $Z$로 변환한 후 $Z$값이 $z_a$보다 큰지를 검토
- 크다면 귀무가설 기각
- 그렇지 않다면 귀무가설 채택
검정의 단계
- $H_0$, $H_1$ 설정
- 유의수준 $\alpha$ 설정
- 검정통계량 계산
- 기각역(검정통계량의 범위) 또는 임계값 계산
- 주어진 데이터로부터 유의성 판정
모평균의 검정
대립가설
- 문제에서 검정하고자 하는 것이 무엇인지 파악 필요
- 대립가설 $H_1$채택을 위한 통계적 증거 확보 필요
- 증거가 없으면 귀무가설 $H_0$ 채택
- $H_1 : \mu > \mu_0$ : 모평균이 뮤제로보다 크다
- $H_1 : \mu < \mu_0$
- $H_1 : \mu != \mu_0$
- 어떤 농장에서 생산되는 계란의 평균 무게는 10.5그램으로 알려져 있다. 새로운 사료를 도입한 후에 생산된 계란 30개의 표본 평균을 계산했더니 11.4그램이 나왔다. 새로운 사료가 평균적으로 더 무거운 계란을 생산한다고 할 수 있는가?
- $H_0 : \mu = 10.5$
- $H_1 : \mu > 10.5$
- 어떤 농장에서 생산되는 계란의 평균 무게는 10.5그램으로 알려져 있다. 새로운 사료를 도입한 후에 생산된 계란 30개의 표본 평균을 계산했더니 9.4그램이 나왔다. 새로운 사료가 평균적으로 더 가벼운 계란을 생산한다고 할 수 있는가?
- $H_0 : \mu = 10.5$
- $H_1 : \mu < 10.5$
- 어떤 농장에서 자신들이 생산하는 계란의 평균 무게가 10.5그램이라고 홍보하고 있다. 이에 생산된 계란 30개의 표본 평균을 계산했더니 9.4그램이 나왔다. 이 농장의 광고가 맞다고 할 수 있는가?
- $H_0 : \mu = 10.5$
- $H_1 : \mu != 10.5$
검정통계량
- n >= 30인 경우
- 중심극한 정리 사용(s: 표본표준편차)
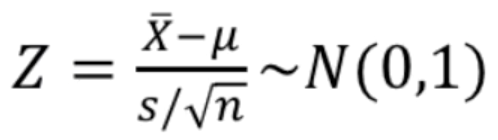
- 모집단이 정규 모집단이고, 모표준편차 $\sigma$가 주어진 경우
기각역
기각역은 대립가설이 무엇인가에 따라서 범위가 달라진다.
- $H_0 : \mu = 10.5$
- 유의수준 : $\alpha$
- 기각역
- $H_1 : \mu > 10.5$ -> $Z > z_a$
- $H_1 : \mu < 10.5$ -> $Z < z_a$
- $H_1 : \mu != 10.5$ -> $|Z| > z_{a/2}$
기각역은, 정규분포 그래프를 그렸을때 양 극단의 $z_a$값 이하/이상의 부분(그래프에서 양 끝단의 부분들)에 해당되는지 보는 것이다. 기각역에 해당되면 귀무가설이 탈락된다.
import numpy as np w = [10.7, 11.7, 9.8, 11.4, 10.8, 9.9, 10.1, 8.8, ...] mu = 10.5 xbar = np.mean(w) sd = np.std(w, ddof=1) print("평균 %.2f, 표준편차: %.2f" %(xbar,sd)) z = (xbar-mu)/(sd/np.sqrt(len(w))) print("검정통계량: ", z) alpha = 0.05 import scipy.stats cri = scipy.stats.norm.ppf(1-alpha/2) print("임계값: ", cri)