[인공지능 수학 - 자료의 정리]10강 : 통계학, 기본개념
개념 정의
- 통계학(statistics)
- 데이터의 수집(collection), 구성(organization), 분석(analysis), 해석(interpretation), 표현(presentation)에 관한 학문
- 기술통계학(descriptive statistics)
- 추측통계학(inferential statistics)
- 모집단(population)
- 어떤 질문이나 실험을 위해 관심의 대상이 되는 개체나 사건의 집합
- 전교 남학생의 키
- 모수(parameter)
- 모집단의 수치적인 특성
- 키의 평균
- 표본(sample)
- 모집단에서 선택된 개체나 사건의 집합 우리가 보통 알고 싶어하는 것은 모수이다. 보통 모집단은 너무 방대하기 때문에, 모집단의 표본을 선택해 그 표본의 모수를 알아내어 모집단의 특성을 알고자 한다.
도수(Frequency)
- 정의
- 어떤 사건이 실험이나 관찰로부터 발생한 횟수
- 표현 방법
- 도수분포표(Frequency Distribution Table)
- 막대그래프(Bar graph)
- 질적 자료(수치가 아닌 범주로 구분되는 자료 : 남/녀, 책의 종류)
- 히스토그램(Histogram)
- 양적 자료(수치적으로 구분되는 자료 : 남학생의 키)
- 질적 데이터
- A A A A A A A A A A B B B B B B C C C C C C D D D D D D D D D D D E E E E E E E F F F F G G G G G G G H H H H
- 도수분포표
| A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|
| 10 | 6 | 6 | 10 | 7 | 4 | 7 | 4 |
-
막대그래프
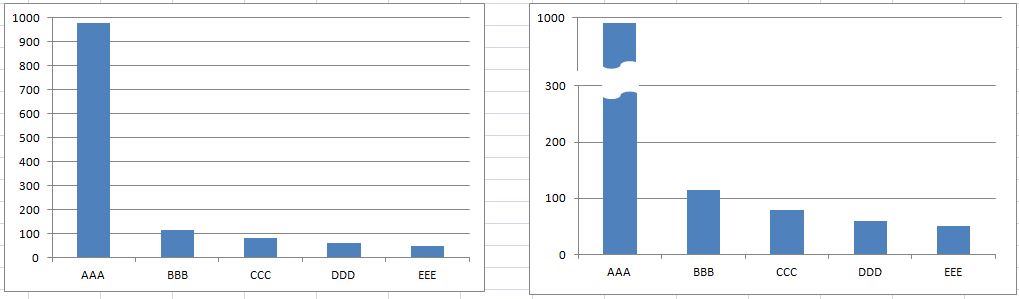
- 양적데이터
- 3.600 1.800 3.333 2.283 4.533 2.883 4.733 ..
- 히스토그램
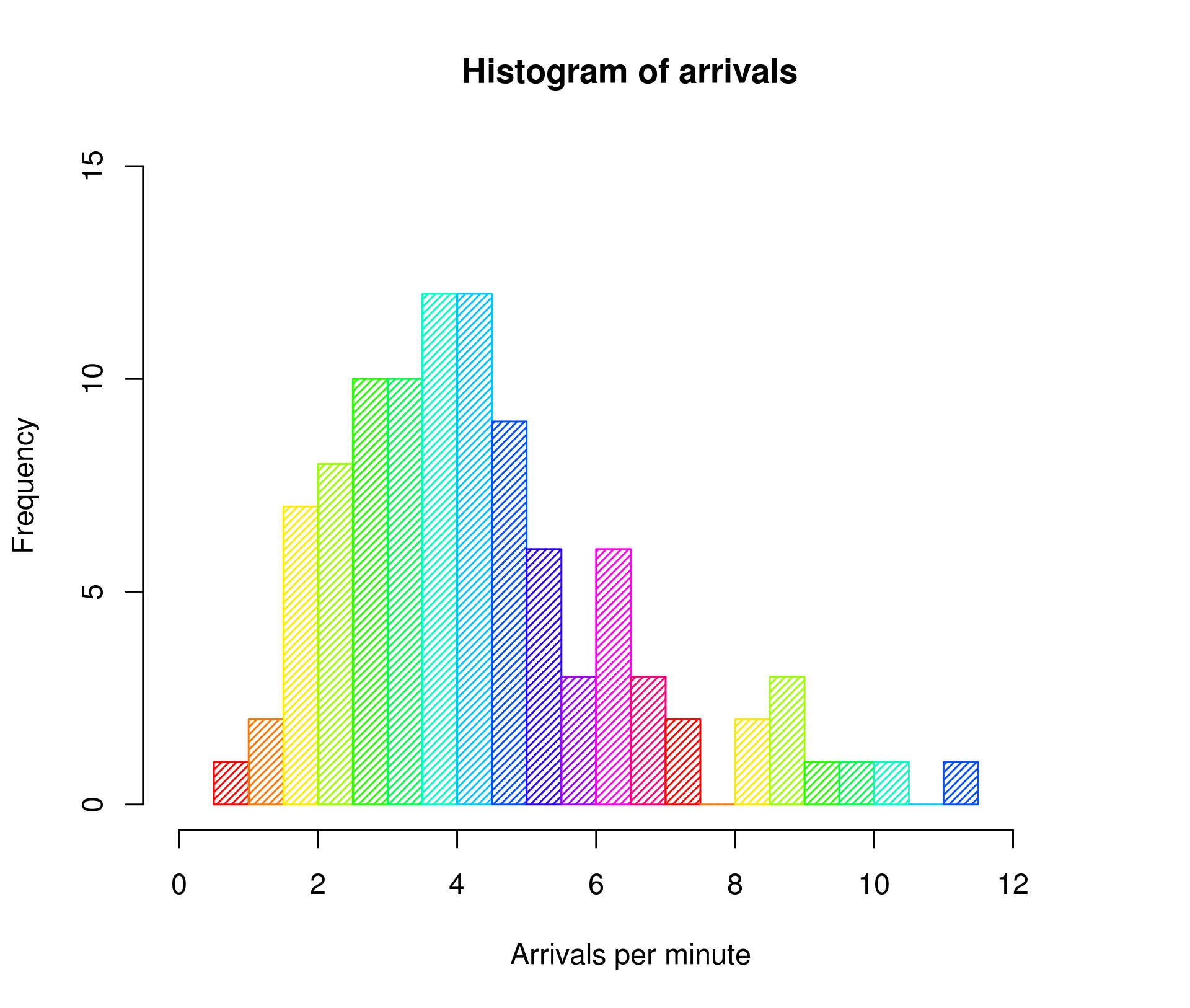
막대그래프와 다르게 히스토그램은 x축 값의 순서가 의미가 있다. x축 값의 순서를 바꿔서는 안된다.
줄기-잎 그림
- Stem and Leaf Diagram
- 양적 자료를 줄기와 잎으로 구분
- 양적 자료를 소팅한 뒤 숫자의 앞부분(기준은 정하기 나름)을 Stem, 뒷부분을 Leaf으로 한다.
- 아래 그림은 1.6, 1.8, 2.0 …을 Stem으로 하여 정리한 줄기-잎 그림이다.
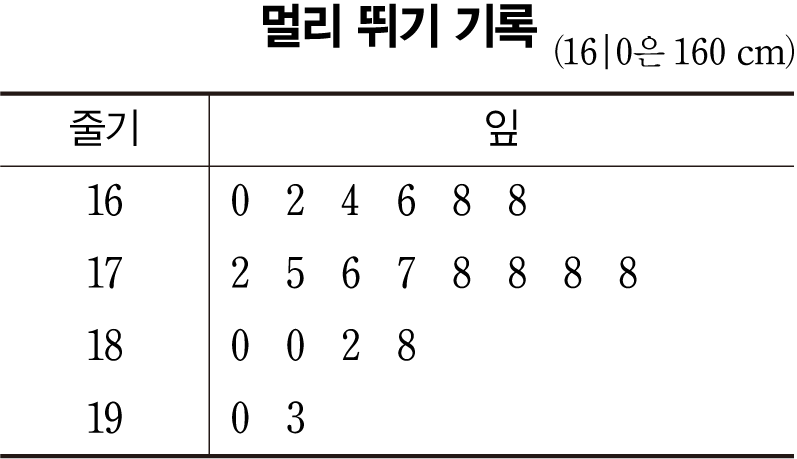
- R 패키지, 파이썬 등으로 쉽게 그릴 수 있다.
상대도수
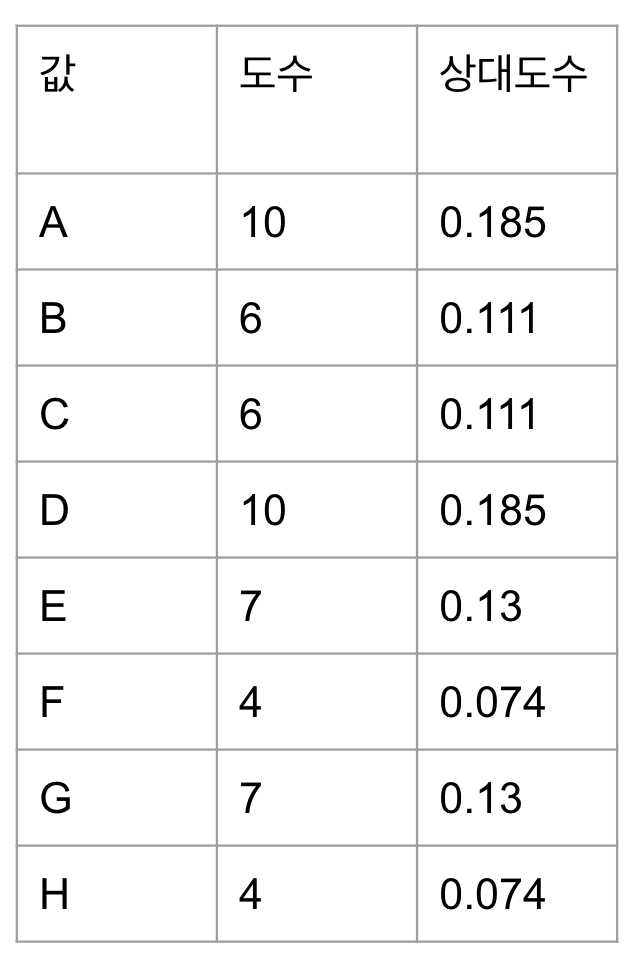
- 도수를 전체 원소의 수로 나눈 것
- 아래 표에서 전체 개수는 54이다. 각 도수를 54로 나누면 상대도수가 된다.
scipy 모듈
데이터를 수집하고 특성을 파악하기 위한 scipy 모듈!
우분투에서 설치하는 방법
sudo apt-get install python3-numpy python3-scipy
python3-matplotlib python3-pandas python3-sympy
python3-nose
mac에서는
pip3 install --user scipy
평균
- mean
${x_1 + x_2 + \dots + x_n \above 1pt n} = {1 \above 1pt n} \sum_{i=1}^n x_i$>>> a = [79, 54, 74, 62, 85, 55, 88, 85, 51, 85, 54, 84, 78, 47] >>> len(a) 14 >>> import statistics >>> statistics.mean(a) 70.07142857142857평균을 구하는 것은 파이썬에 이미 내장되어 있어서 scipy를 쓰지 않아도 가능하다.
- 모평균 $\mu$
- 모집단 전체 자료일 경우
- 표본 평균 $\bar{x}$
- 모집단에서 추출한 표본일 경우
중앙값 (Median)
- 평균의 경우 극단 값의 영향을 많이 받음
>>> a = [79, 54, 74, 62, 85, 55, 88, 85, 51, 85, 54, 84, 78, 47, 1000] >>> statistics.mean(a) 132.06666666666666이런 경우 평균보다 중앙값이 더 좋은 역할을 하게 된다.
- Median
- 주어진 자료를 높은 쪽 절반과 낮은 쪽 절반으로 나누는 값을 의미
- 자료를 순서대로 나열했을 때 가운데 있는 값
- 자료의 수 : n
- n이 홀수 : (n+1)/2번째 자료값
- n이 짝수 : n/2 번째와 (n/2)+1번째 자료값의 평균
>>> a = [79, 54, 74, 62, 85, 55, 88, 85, 51, 85, 54, 84, 78, 47] >>> b = [79, 54, 74, 62, 85, 55, 88, 85, 51, 85, 54, 84, 78, 47, 1000] >>> a = sorted(a) >>> a [47, 51, 54, 54, 55, 62, 74, 78, 79, 84, 85, 85, 85, 88] >>> b = sorted(b) >>> b [47, 51, 54, 54, 55, 62, 74, 78, 79, 84, 85, 85, 85, 88, 1000] >>> statistics.median(a) 76.0 # a에서 74와 78의 평균 >>> statistics.median(b) 78 # b에서 의 중앙값 78
분산(Variance)
- 편차의 제곱의 합을 자료의 수로 나눈 값
- 편차 : 값과 평균의 차이
- 자료가 모집단일 경우 : 모분산 $\sigma^2 = {1 \above 1pt N} \sum_{i=1}^N (x_i - \mu)^2$
- 자료가 표본일 경우 : 표본분산 $s^2 = {1 \above 1pt n-1} \sum_{i=1}^n (x_i - \bar {x})^2$
값들이 평균에서 많이 떨어져 있을수록 분산이 크게 나온다. 아래와 같이 파이썬에서 표본분산을 구해볼 수 있다.
>>> statistics.variance(a)
234.37912087912088
>>> statistics.variance(b)
57868.78095238096 # 1000이라는 이상점으로 인해 분산이 크게 나온다.
>>> import scipy
>>> import scipy.stats
>>> scipy.stats.tvar(a)
234.37912087912085
표준편차(Standard Deviation)
- 분산의 양의 제곱근
- 모표준편차(population standard deviation) $\sigma^2 = \sqrt{1 \above 1pt N} \sum_{i=1}^N (x_i - \mu)^2$
- 표본표준편차(sample standard deviation)
$s^2 = \sqrt{1 \above 1pt n-1} \sum_{i=1}^n (x_i - \bar {x})^2$
파이썬으로 계산하면 다음과 같다. - 표준편차
>>> statistics.stdev(a) 15.30944547915178 >>> statistics.stdev(b) 240.55930859640614 - 모분산, 모표준편차
>>> statistics.pvariance(a) 217.6377551020408 >>> statistics.pstdev(a) 14.752550799846134numpy를 사용해서 모분산, 모표준편차를 구하면 다음과 같다.
>>> import numpy >>> numpy.var(a) 217.63775510204079 >>> numpy.std(a) 14.752550799846134ddof=1을 붙여주면 각각 표본분산과 표본표준편차를 구할 수 있다.
ddof : Delta Degrees of Freedom>>> numpy.var(a, ddof=1) 234.37912087912085 >>> numpy.std(a, ddof=1) 15.30944547915178
범위(Range)
- 자료를 정렬하였을 때 가장 큰 값과 가장 작은 값의 차이
python에서 제공하는 max, min 혹은 numpy를 써도 된다.>>> max(a) - min(a) 41 >>> max(b) - min(b) 953 >>> numpy.max(a) - numpy.min(a) 41
사분위수(Quantile)
- 전체 자료를 정렬했을 때 1/4, 1/2, 3/4 위치에 있는 숫자
- Q1 : 제 1 사분위수
- Q3 : 제 3 사분위수
>>> numpy.quantile(a, .25) 54.25 >>> numpy.quantile(a, .5) 76.0 >>> numpy.quantile(a, .75) 84.75 >>> numpy.quantile(a, .60) # 1/4, 1/2, 3/4이 아닌 값이 들어가기도 한다. 소팅을 했을 때 60%에 해당하는 숫자를 알려준다. 이 결과의 숫자 앞으로 60%의 수가, 뒤로 40%의 수가 있음을 알 수 있다. 78.8
- 사분위범위(IQR, interquartile range)
- Q3 - Q1
>>> numpy.quantile(a, .75) - numpy.quantile(a, .25) 30.5 >>> numpy.quantile(b, .75) - numpy.quantile(b, .25) 30.5
- Q3 - Q1
- z-score
- 어떤 값이 평균으로부터 몇 표준편차 떨어져 있는지를 의미하는 값
- 모집단의 경우 $z = {x - \mu \above 1pt \sigma}$
- 표본의 경우 $z = {x - \bar {x} \above 1pt s}$
- a에 대한 모집단에 대해 z-score를 계산하면 다음과 같다.
>>> scipy.stats.zscore(a) array([-1.5638942 , -1.29275464, -1.08939998, -1.08939998, -1.02161509, -0.54712088, 0.26629777, 0.53743732, 0.60522221, 0.94414665, 1.01193154, 1.01193154, 1.01193154, 1.2152862 ]) - 표본표준편차로 계산했을 때의 z-score를 계산하면 다음과 같다.
>>> scipy.stats.zscore(a, ddof=1) array([-1.50700616, -1.24572955, -1.04977209, -1.04977209, -0.98445294, -0.52721887, 0.25661096, 0.51788756, 0.58320672, 0.90980248, 0.97512163, 0.97512163, 0.97512163, 1.17107909])
