[인공지능 수학 - 확률과 확률분포]12강 : 확률-2
이항분포
- 베르누이 시행(Bernoulli trial)
- 정확하게 2개의 결과만을 가지는 실험
- 예) 동전 던지기
- 보통 성공과 실패로 결과를 구분
- 성공의 확률 : $p$
- 정확하게 2개의 결과만을 가지는 실험
- 확률변수 $X$
- n번의 베르누이 시행에서 성공의 횟수. 자연수로 나옴.
- 이항확률변수라고 함
- 이항분포(binomial distribution)
- 이항확률변수의 확률분포
-
이항 확률변수 X의 확률분포
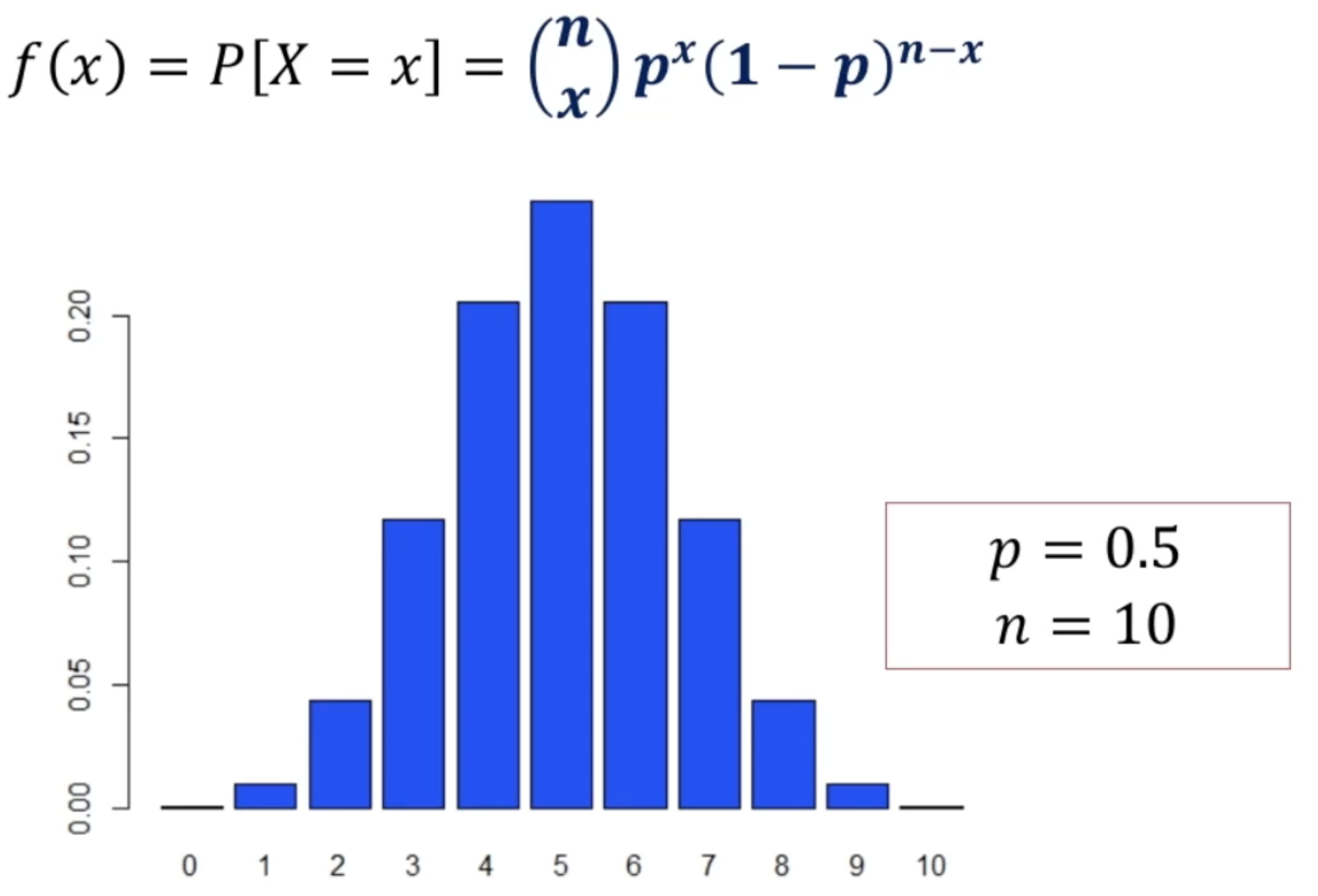
x축이 n, y축이 p - 어떤 랜덤박스의 뽑기 성공 확률이 0.2이다.
- 3개를 뽑았을 때, 적어도 하나 이상의 성공이 발생할 확률은?
$P[X \geq 1] = 1 - P[X = 0] = 1 - \binom{3}{0}(0.2)^0(1-0.2)^{3 - 0} = 1 - 0.512 = 0.488$
>>> from scipy import stats >>> 1 - stats.binom.cdf(0, n=3, p=0.2) 0.4879999999999999stats.binom.cdf(0, n=3, p=0.2)에서,
- 0 : 0보다 같거나 작은 확률을 cdf가 제공한다.
- 3 : 베르누이 시행을 몇번 하는지
-
0.2 : 성공의 확률 그럼 binom을 통해 이항분포를 계산해준다!
- 평균
- $E(X) = np$
- 분산
- $Var(X) = np(1 - p)$
- 표준편차
- $SD(X) = \sqrt {np(1 - p)}$
다음은 stats로 이항분포의 평균과 분산을 구한 것이다.
>>> stats.binom.stats(n=3, p=0.2) (array(0.6), array(0.48)) # 각각 평균, 분산
- $SD(X) = \sqrt {np(1 - p)}$
다음은 stats로 이항분포의 평균과 분산을 구한 것이다.
정규분포
지금까지 본 분포들은 이산확률분포였다. 각각의 확률변수가 갖고 있는 값들이 셀 수 있는 값들이었다. 정규분포는 이와 다르게 연속확률분포를 가진다. 확률변수 X가 가지는 값을 셀 수가 없다.
- 연속활률 변수의 확률 분포
- 확률밀도함수(probability density function)
- $f(x)$
- $P[a \leq X \leq b] = \int_{b}^{a}f(x)dx$
- 즉 그래프 아래 부분의 넓이가 확률이 됨
- 어떤 구간에 대한 확률을 알 수 있다.
- 확률밀도함수(probability density function)
-
정규분포의 확률밀도함수
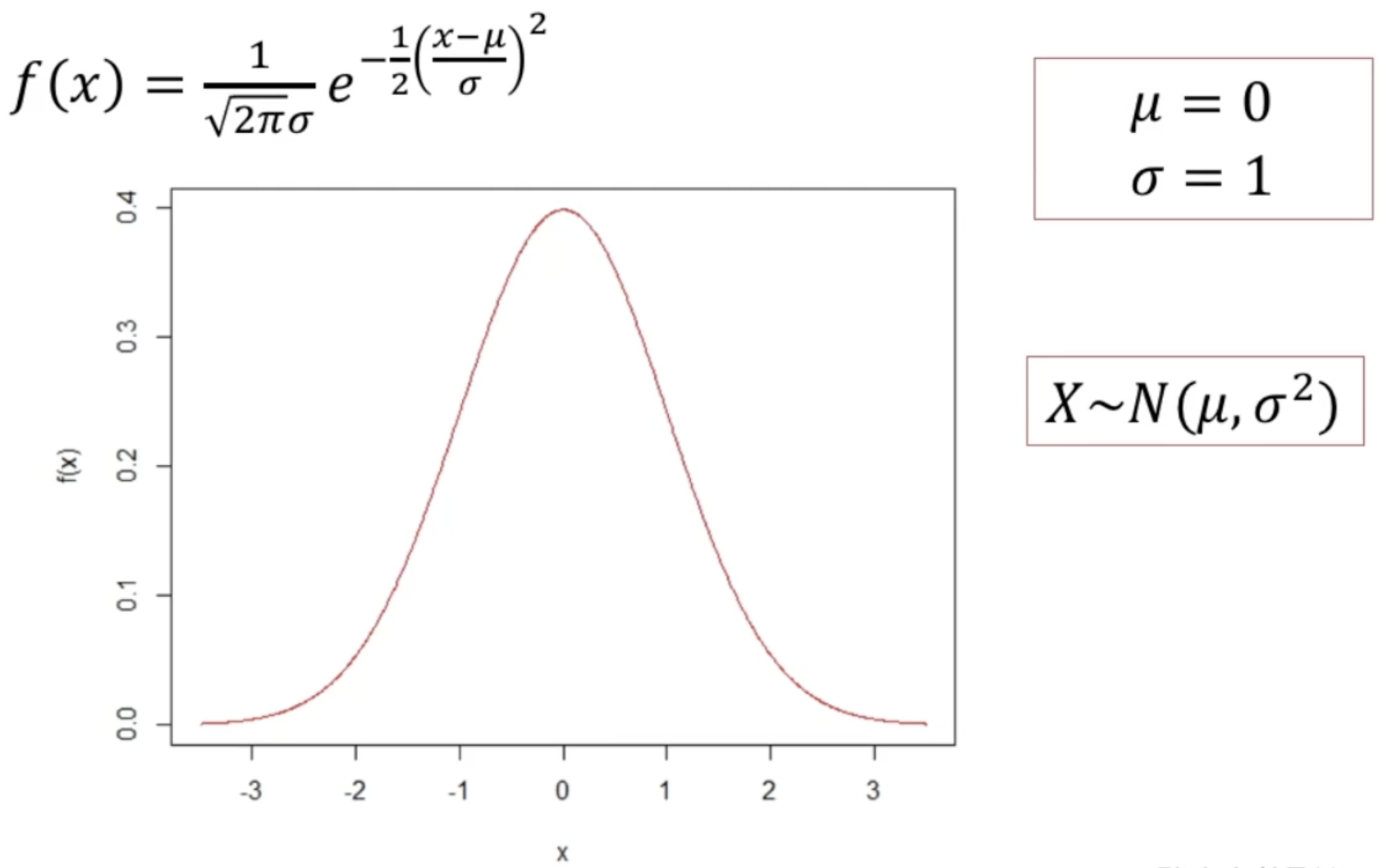
$\sigma$, $\mu$가 중요한 파라미터이다.
이 식은 적분이 안된다.
$x = \mu$일 때, $f(x)$의 값이 가장 큰 것을 볼 수 있다.
$\sigma$가 커질수록 그래프가 양쪽으로 퍼지게 된다. - 표준정규확률변수
- standard normal random variable
- $Z = {X - \mu \above 1pt \sigma}$
- standard normal random variable
- 표준정규분포
- standard normal distribution
- $Z$ ~ $N(0,1)$ # 평균이 0, 시그마 제곱이 1
- 표준 정규분포표
- $P[Z \leq z]$
모든 정규확률변수는 표준정규확률변수로 변환이 가능하다.
- $P[Z \leq z]$
$X ~ N(4,3^2)$
- $P[x\leq 4]=?$
$= P[{X-\mu \above 1pt \sigma }\leq {4-\mu \above 1pt \sigma}] = P[Z \leq {4-4 \above 1pt 3}] = P[Z\leq 0] = 0.5$
X는 정규확률변수이다. 평균이 4, 분산이 3의 제곱이다.
이때, X가 4보다 작은 확률을 구해라. 표준정규확률분포표에서 이를 구하기 위해서는, 정규확률변수 X를 표준정규확률변수 Z로 치환해야 한다. 치환한 후의 값을 표준정규확률분포표(구글링하면 많이 나온다)에서 찾아서 쓰면 된다.
>>> stats.norm.cdf(4, loc=4, scale=3)
0.5
파이썬에서는 표준졍규확률변수로 변경할 필요 없이, 파라미터 값만 잘 넣어주면 된다. 맨 앞의 4는 $P[X \leq 4]$에서 4보다 작은 평균을 구하기 위함이고, loc는 평균, scale은 분산이다.(분산은 표준편차의 제곱이므로! 3^2가 아닌 3만 써주면 됨!)
$X ~ N(4, 3^2)$
- $P[4\leq X\leq 7] = ?$
$P[X\leq 7] - P[X< 4] = P[Z \leq {7-4 \above 1pt 3}] - P[Z < 0] = P[Z \leq 1] - P[Z < 0] = 0.8413 - 0.5 = 0.3413$
이런 경우 두개의 사건으로 분리할 수 있다.
7보다 작을 사건의 확률 - 4보다 작을 사건의 확률
그리고 표준정규확률변수 Z로 치환해준다. 치환한 후의 값을 표준정규확률분포표(구글링하면 많이 나온다)에서 찾아서 쓰면 된다.
>>> stats.norm.cdf(7, loc=4, scale=3) - stats.norm.cdf(4, loc=4, scale=3)
0.3413447460685429
- 어떤 종목의 주가는 전달 종가를 평균으로 하고, 표준편차가 50인 정규분포를 따른다고 한다.
- 오늘 종가가 1000원일 때, 내일 주가가 1100원 이상이 될 확률은?
$P[X \geq 1100] = P[Z \geq {1100-1000 \above 1pt 50}] = P[Z\geq 2] = 1-P[Z < 2] = 1 - 0.9772 = 0.0228$
마찬가지로 정규확률변수 X를 표준정규확률변수 Z로 치환한다. 평균은 1100, 표준편차는 50으로 계산한다.>>> 1 - stats.norm.cdf(1100, loc=1000, scale = 50) 0.02275013194817921
포아송 분포
- Poisson distribution
- 일정한 시간단위 또는 공간 단위에서 발생하는 이벤트의 수의 확률분포
- 하루 동안 어떤 웹사이트를 방문하는 방문자의 수
- 어떤 미용실에 한 시간동안 방문하는 손님의 수
- 어떤 전기선 100미터당 발생하는 결함의 수
- 확률분포함수(확률질량함수)
- $P[X = x] = f(x) = \lambda^x {e^-\lambda \above 1pt x!}$, $x = 0, 1, 2, \dots$
- 평균 : $\lambda$
- 분산 : $\lambda$
- 어느 웹사이트에 시간당 접속자 수는 평균이 3($\lambda = 3$)인 포아송 분포를 따른다고 한다.
- 앞으로 1시간 동안 접속자 수가 2명 이하일 확률은?
- $P[X \leq 2] = ?$
앞에서 배운 확률분포함수(확률질량함수)에 x가 0, 1, 2일때를 넣어서 구하면 된다!
$P[X \leq 2] = P[X = 0]+P[X = 1] + P[X=2] = 3^0{e^{-3} \above 1pt 0!} + 3^1{e^{-3} \above 1pt 1!} + 3^2{e^{-3} \above 1pt 2!} = 0.04998 + 0.14936 + 0.22404 = 0.42319$>>> stats.poisson.cdf(2, mu=3) 0.42319008112684364포아송 분포를 이처럼 파이썬으로 쓸 수 있다.
2는 2보다 작을때의 확률을 구하는것, mu=3은 평균(람다)이다.
포아송 분포에서, 람다만 결정이 되면 분산도 결정이 되고, 확률분포 함수 자체도 결정이 된다.
지수분포
- exponential distribution
- 포아송 분포에 의해 어떤 사건이 발생할 때, 어느 한 시점으로부터 이 사건이 발생할 때까지 걸리는 시간에 대한 확률 분포
- 확률밀도 함수
- $f(t) = \lambda e^{-\lambda t}$
- $\lambda$ : 포아송분포의 평균
- 평균
- $E(T) = {1 \above 1pt \lambda}$
- 분산
- $Var(T) = {1 \above 1pt \lambda^2}$
- 어느 웹사이트에 시간당 접속자 수는 $\lambda = 3$인 포아송 분포를 따른다고 한다.
- 지금부터 시작하여 첫번재 접속자가 30분 이내에 올 확률은?
- $P[T \leq 0.5] = ?$
T는 시간단위이므로 30분은 0.5라고 한다. 즉, 0부터 0.5까지 확률밀도함수를 적분한다.
$P[T \leq 0.5] = \int_{0}^{0.5}\lambda e^{-\lambda t}dt = \int_{0}^{0.5}3e^{-3t}dt = [-e^{-3t}]_{0}^{0.5} = 1 - e^{-1.5} = 1 - 0.2231 = 0.7769$>>> lam = 3 >>> stats.expon.cdf(0.5, scale=1/lam) 0.77686983985157020.5는 30분 이내의 확률, scale은 표준편차.
