[Machine Learning 기초]확률이론

Machine Learning 기초

Machine Learning 소개

Machine Learning이란?

Machine Learning(기계학습)

• 경험을 통해 자동으로 개선하는 컴퓨터 알고리즘의 연구
• 학습데이터: 입력벡터들 $x_1, …, x_N$, 목표값들 $t_1, …, t_N$
• 머신러닝 알고리즘의 결과는 목표값을 예측하는 함수 y(x)
  

예제 : 숫자 인식

MNIST 데이터의 경우 $28 * 28$ 숫자 array로 표현된다.

핵심개념들

• 학습단계(training or learning phase): 함수y(x)를 학습데이터에 기반해 결정하는 단계
• 시험셋(test set): 모델을 평가하기 위해서 사용하는 새로운 데이터
  • 궁극적인 목표인 새로운 데이터에 대한 예측을 하기 위해 시험셋으로 시뮬레이션 한다.
  • 시험셋을 들여다보면 안된다! 시험셋을 통해 정확도를 높이려는 작업을 하면 실제 상황에서는 잘 작동하지 않을 가능성이 높다.
• 일반화(generalization): 모델에서 학습에 사용된 데이터가 아닌 이전에 접하지 못한 새로운 데이터에 대해 올바른 예측을 수행하는 역량
• 지도학습(supervised learning): target이 주어진 경우. 가장 많이 쓰이는 경우이다.
  • 분류(classification)
  • 회귀(regression)
• 비지도학습(unsupervised learning): target이 없는 경우
  • 군집(clustering)

우리가 여기서 다룰 문제들을 대부분 지도학습 문제들이다.

다항식 곡선 근사(Polynomial Curve Fitting)

• 지도학습의 회귀 문제에 해당한다.
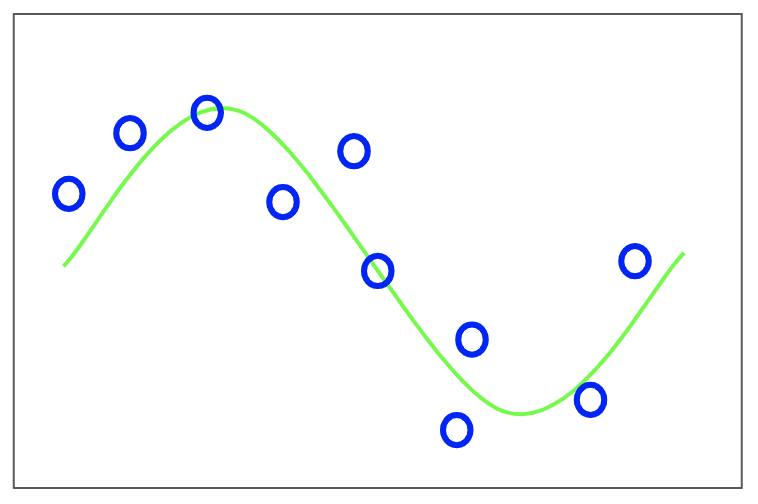
  sin함수이다. x가 0에서1까지 변할때의 곡선이고, 0과 1 사이에서 랜덤한 x값을 생성한다.
  y축은 t값인데, 랜덤한 노이즈를 더해서 생성한다.
  10개의 파란 점이 녹색 선을 조금씩 벗어나 있다. 벗어난 이유는 sin함수값에 랜덤한 노이즈를 더했기 때문이다.
  
  

• 학습데이터: 입력벡터 $X = (x_1, …, x_N)^T, t = (t_1, …, t_N)^T$
  • X는 N개의 입력값, t는 N개의 타겟(목표)값이다.
  • T는 행벡터를 열벡터로 바꿔준 것이다.
• 목표: 새로운 입력벡터 x hat가 주어졌을 때 목표값 t hat을 예측하는 것
• 확률이론(probability theory): 예측값의 불확실성을 정량화시켜 표현할 수 있는 수학적인 프레임워크를 제공한다.

• 결정이론(decision theory): 확률적 표현을 바탕으로 최적의 예측을 수행할 수 있는 방법론을 제공한다.
  
  

• A Polynomial function linear in w
  우리가 사용할 함수 y는 x가 입력, w가 모델 파라미터로 주어진다. w는 계수, 모델 파라미터라고 부른다. 여기서는 M+1개의 모델 파라미터가 있음을 알 수 있다.
  x에 대해서 다항식이 된다. w에 대해서는 선형식이 된다.
  이것을 잘 구분하는것이 중요하다.
  x는 데이터에서 주어지는 값이고 계속 바뀔 수 있다. w같은 경우 고정되어 있는 값이다.
  우리의 목표는 고정되어있지만 알지 못하는 w의 값을 찾아내는 것이다.
  
  

오차함수(Error Function)

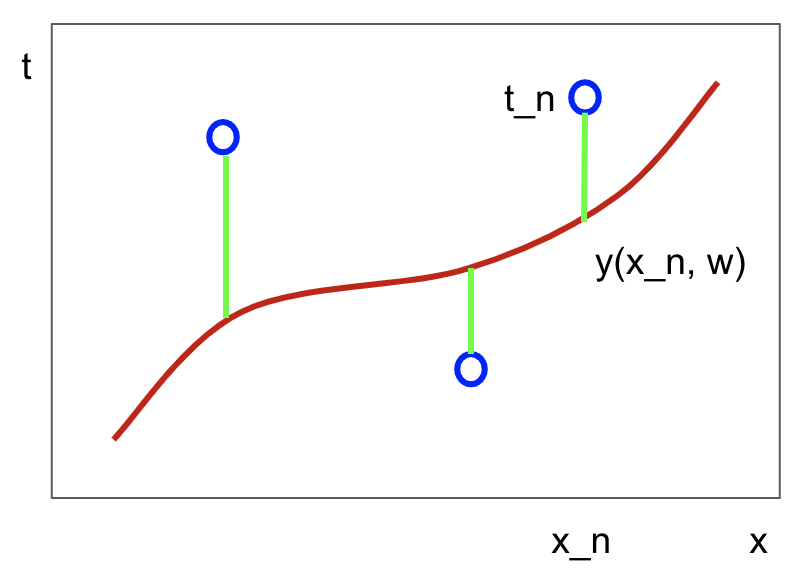
$E(w) = {1 \above 1pt 2}\sum_{n=1}^{N}{y(x_n, w) - t_n}^2$
주어진 w에 대한 함수값 y와 데이터에서 주어진 t값 사이의 차이를 표현한다. 이 차이를 오차함수라고 한다.
오차함수들 중에서 가장 일반적인 함수는 오차의 제곱합 함수이다. 이는 w에 대한 함수이다. 1/2는 수식을 간단하게 하기 위해 곱한다.
제곱을 하기 때문에 E라는 이 함수는 항상 양수가 된다. 목표값과 예측값이 같으면 0이 된다.

과소적합(Under-fitting)과 과대적합(Over-fitting)

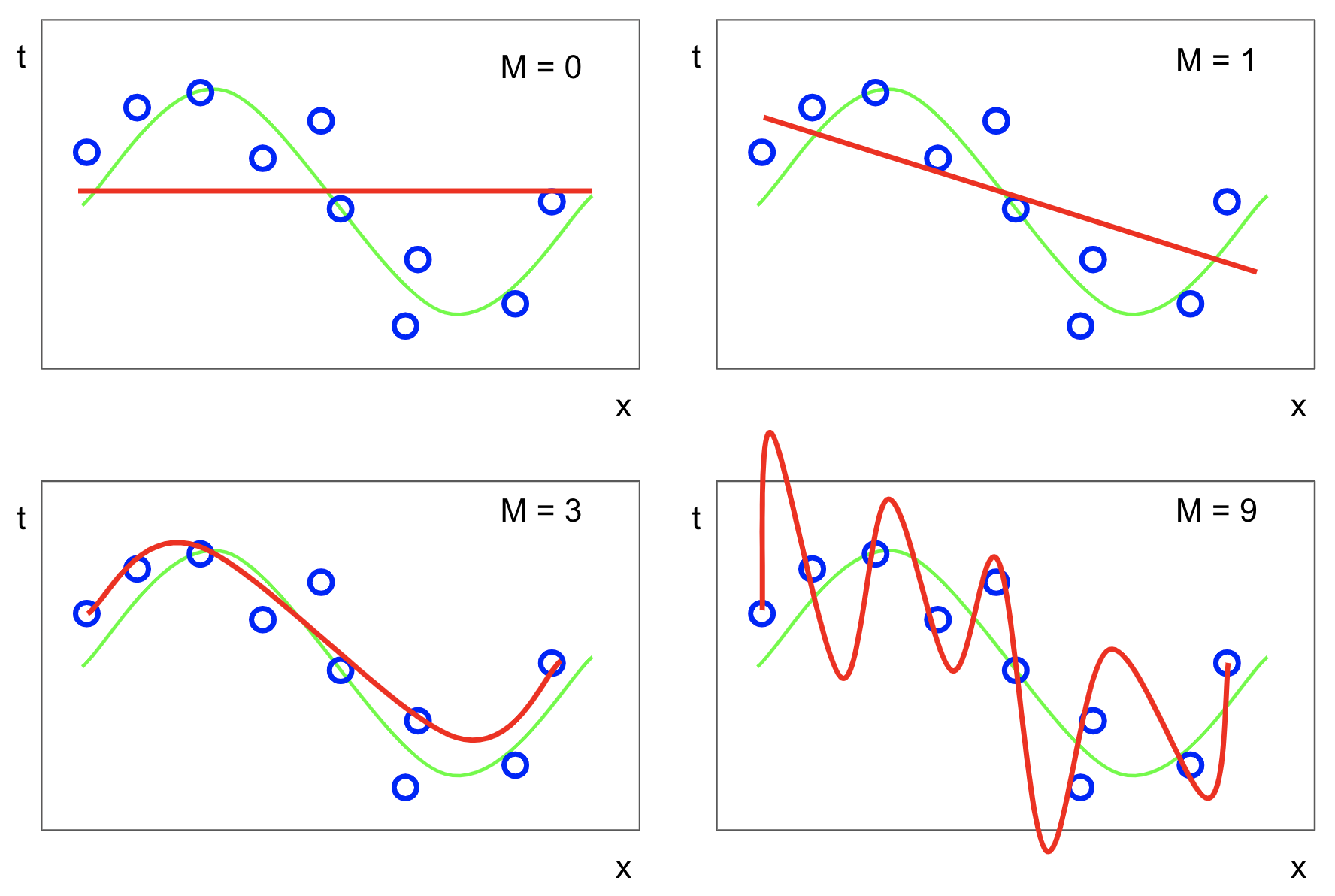
M의 값을 결정해야 한다.
M값에 따라 1차식, 2차식 등등 형태가 바뀐다.
M=0이면 기울기가 없는 직선이 된다. 좋지 않은 모델이다. 이를 과소적합이라고 한다.
M=1이면 기울기는 있지만 여전히 직선이다. sin함수를 제대로 근사하고 있지 못하므로 과소적합이다.
M=3이면 sin함수에 비슷하게 근사함을 알 수 있다.
M=9이면 곡선의 진동이 너무 심하다. 하지만 곡선이 데이터가 있는 포인트를 모두 정확하게 지나가고 있다. 하지만 점 사이의 변화가 너무 극심하다. 이런 경우는 모델이 데이터의 노이즈까지 너무 무리하게 근사한 것이다. 이런 경우를 과대적합이라고 한다.

E_{RMS} = \sqrt{2E(W^*)/N}
과대적합, 과소적합을 어떻게 판별할 수 있을까?
과대적합, 과소적합은 일반화에 관한 문제이고, 이 모델이 새로운 데이터가 들어왔을 때 잘 예측하는지 알아보는데 유용하다.
시뮬레이션 하기 위해서 학습데이터와 독립된 테스트데이터를 따로 사용한다.
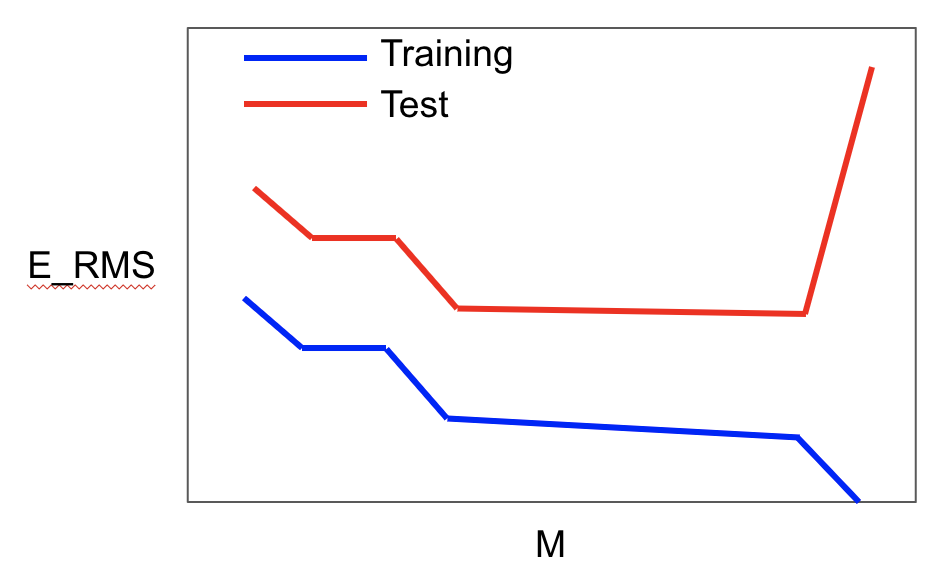
x축은 0부터 9까지 시도한 M의 값, y축은 에러함수의 값이다.
$E_RMS$에서 RMS는 Root Mean Square의 줄임말로, 에러함수를 샘플의개수 N으로 나눈 것이다. 그리고 2를 곱하는데, 이러면 앞서 나왔던 1/2이 사라지게 된다.
모델에 대해 평가할 때 테스트 데이터의 개수가 작은지 많은지에 따라서 두개의 다른 데이터셋을 동일선상에서 비교해주기 위해 $E_RMS$을 사용한다.
그래프를 보면, M이 증가함에 따라 학습데이터와 테스트데이터의 오류가 줄어든다. 3이 되었을때 가장 많이 떨어지고, 그 이후엔 거의 변화가 없다. 하지만 M이 9가 되었을 때, 학습데이터의 에러가 0이 되는데, 테스트데이터의 에러는 기하급수적으로 늘어난다. 이렇게 오버피팅이 되면, 훈련 상에서 가장 좋은 성능을 낸 것이 실제 테스트에서는 가장 나쁜 성능을 보이게 된다.

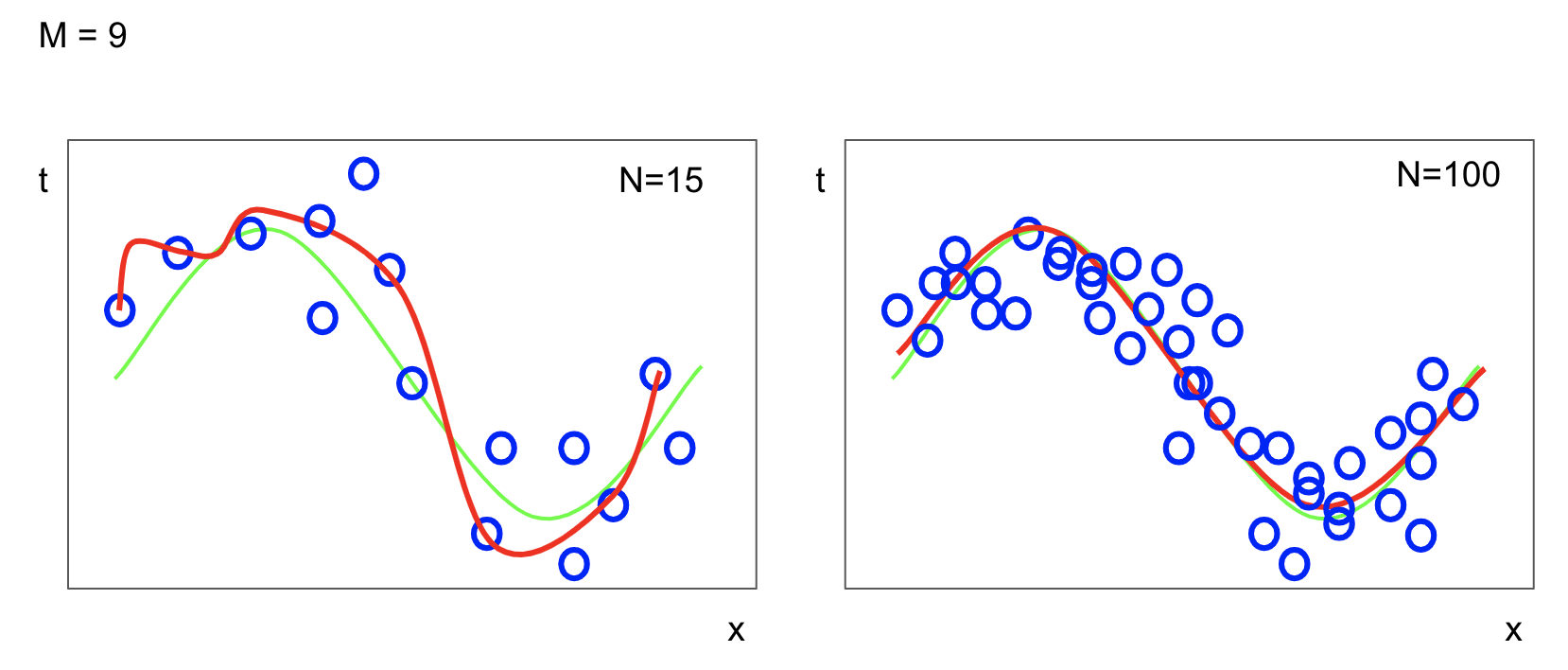
M=9일 경우를 보자. 점들의개수 N이 15인 경우, 똑같이 M=9이지만 이전에 비해 진동이 줄어든 것을 볼 수 있다. N=100일 경우, 훨씬 더 매끈한 곡선에 근사한다.
이를 통해 알 수 있는 것은, 개수가 많아지면 복잡한 모델도 과대적합 문제가 덜 심각해지는 것을 알 수 있다.
즉, 데이터가 많아지면 많아질수록 조금 더 복잡한 모델을 사용해도 된다는 것이다.
모든 머신러닝 프로젝트의 핵심은 많은 양의 데이터를 수집하는 것이다!

규제화(Regularization)

다음의 표는 M의 값의 변화에 따라 계수들(모델 파라미터 값)이 어떻게 변하는지 보여준다.
M이 커질수록 계수의 절대값이 커짐을 알 수 있다. M이 커질수록 학습하는 과정에서 계수값을 키움으로써 데이터를 정확하게 맞추려고 하는 경향이 있다. 밸런스를 맞추기 위해 양수값을 키우는 만큼 음수값도 키운다.
그럼, 계수값이 너무 커지지 않게 제한하면 좋지 않을까? 이것을 위한 게 바로 규제화이다.

가장 간단한 규제화 방법은 절대값이 너무 커지지 않도록 오차함수 안에 처리를 해주는 것이다.

$\widetilde{E}(w) = {1 \above 1pt 2}\sum_{n=1}^{N}{y(x_n, w) - t_n}^2 + {\lambda \above 1pt 2}\left | w \right |^2$
$where \left | w \right |^2 = w^Tw = w_0^2 + w_1^2 + … + w_M^2$
에러함수 위에 물결표시(tilde, 틸다)가 붙는다. 우리가 앞에서 구한 제곱합 에러함수 뒤에 ${\lambda \above 1pt 2} ||w||^2$를 더한다.
람다를 통해 앞부분을 강조할 것인지(더하기 앞부분), w를 작게 만드는 규제화에 집중할 것인지(더하기 뒷부분)을 컨트롤할 수 있다.
람다값이 작으면 작을수록, 원래 우리가 풀었던 제곱합 오차함수를 최소화하는 문제를 푸는 것이다.
람다값이 커지면 커질수록, w값을 작게 만드는 모델을 만들게 된다.
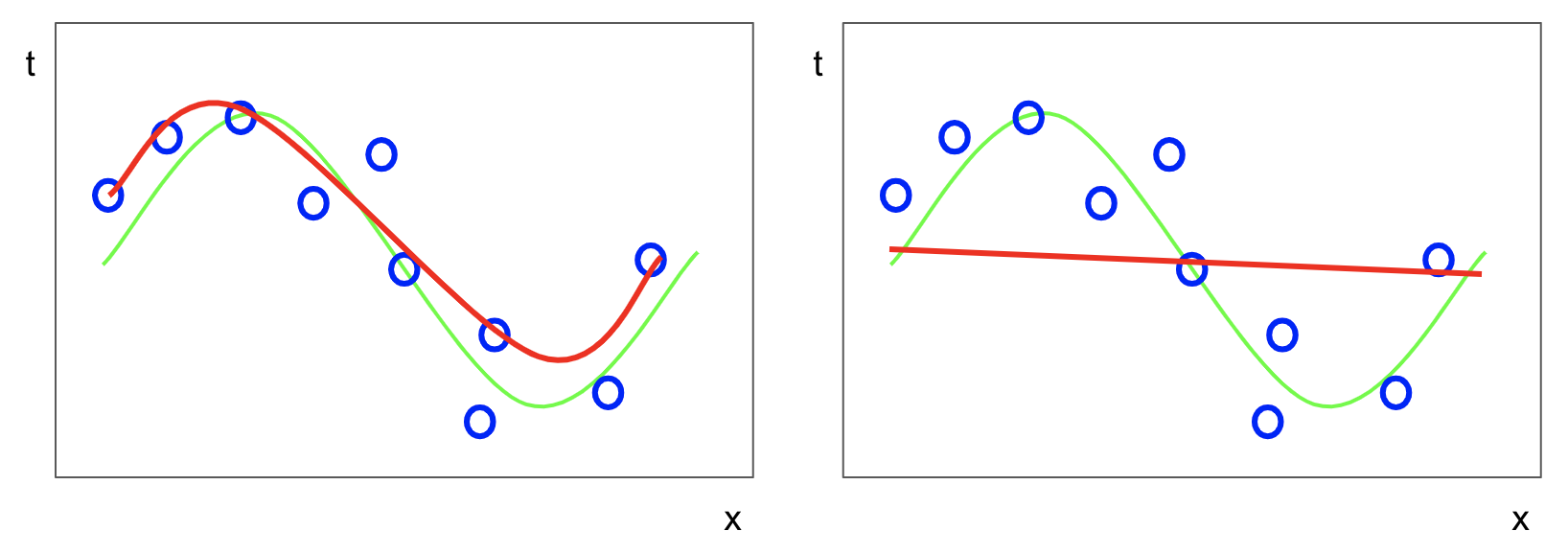
왼쪽 표의 경우, 람다값이 작은 경우이다. 하지만 규제화도 조금 들어가서 데이터개수는 여전히 몇개 안되지만, 앞에서 본 방법에 비해서는 진동이 적은 모델을 만들었다.
오른쪽 표의 경우 람다값이 큰 경우이다. 이 경우에는 너무 규제화에 신경쓰다보니 에러를 해결하지 못해 직선과 같은 형태로 나타난다.
따라서 람다를 너무 크게 하면 과대적합을 피하려다가 과대적합이될 수 있으니 적절한 람다값을 구해야 한다.

몇가지 람다값들을 사용했을 때 계수값들이 어떻게 변하는지 살펴보자.

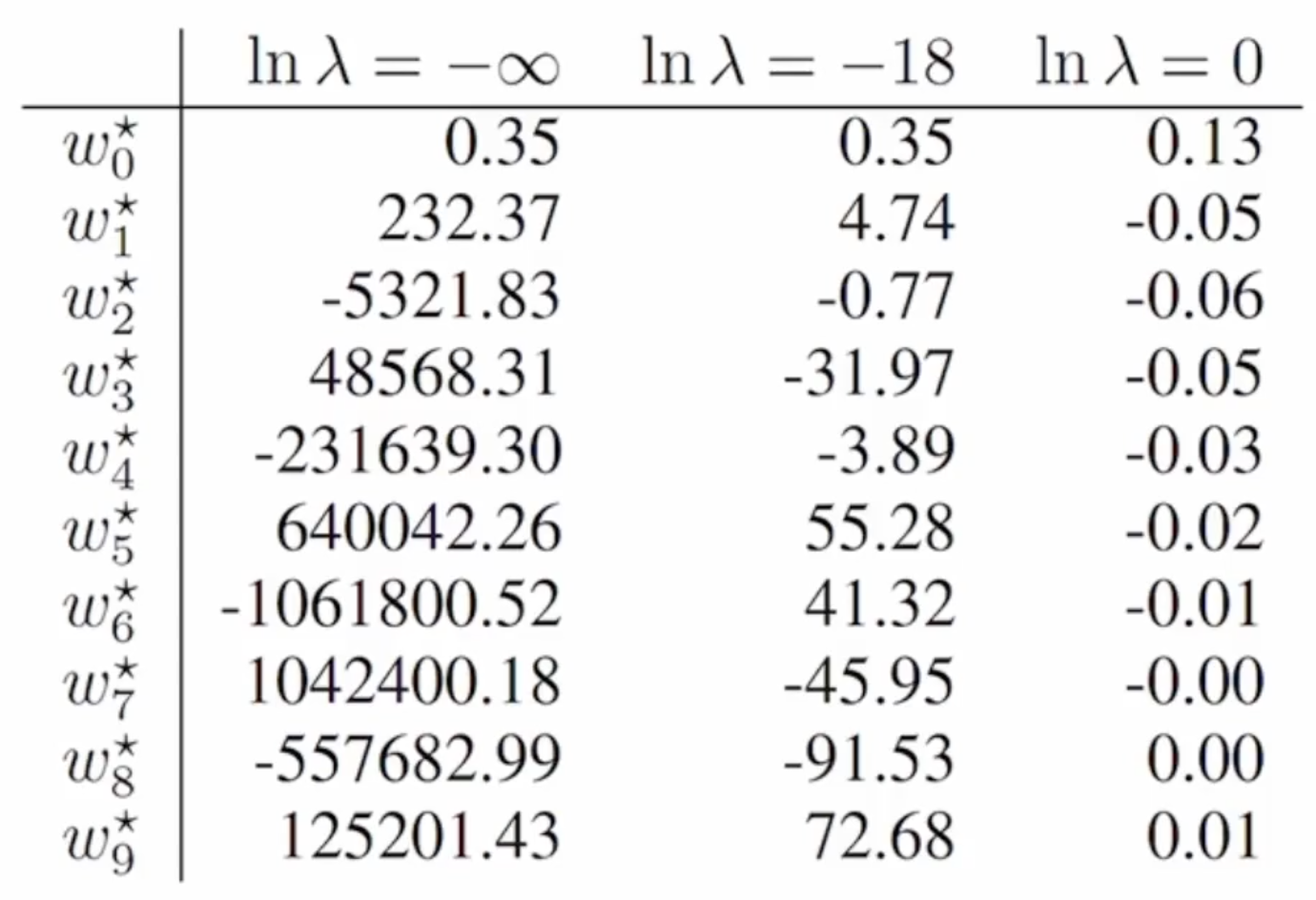
람다가 마이너스 무한, 즉 아주 작아서 규제화를 안한 것이나 다름없는 경우이다. w값의 절대값이 크게 나타난다.
람다가 -18정도로 작은 경우, 어느정도 적절하게 규제화가 된 경우이다. 계수값이 너무 크지도 작지도 않게 나온다.
람다가 0으로 커서 규제화를 너무 많이 한 경우 과소적합이 나타나며 역효과를 일으킨다.

참고 교재소개

• Pattern Recognition and Machine Learning by Christopher Bishop - 대학에서 교재로 많이 쓰임. 머신러닝중에서도 확률에 기반한 부분을 강조한 책
• Deep Learning by lan Goodfellow, Yoshua Bengio and Aaron Courville - 가끔씩 참조할 것
• Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow(2nd Edition) - 머신러닝 프로젝트, 선형회귀, 선형분류할 때 사용할 것
  
  
  

확률이론(Probability Theory)

머신러닝을 이론적으로 이해하는데 있어 필수!

확률변수(Random Variable)

확률변수 $X$는 표본의 집합 $S$의 원소 $e$를 실수값 $X(e) = x$에 대응시키는 함수이다.
즉 확률변수는 확률함수로 정의되어 있다. 표본의 집합이란 여러번 실행을 했을 때 가능한 경우의 수들이다.

• 대문자 $X, Y, …$ : 확률변수
• 소문자 $x, y, …$ : 확률변수가 가질 수 있는 값
• 확률 $P$는 집합 $S$의 부분집합을 실수값에 대응시키는 함수 - $P[X = x]$ - $P[X \leq x]$ - $X = x, X \leq x$는 집합 $S$의 부분집합을 정의한다. 이 표현방법을 잘 기억할 것! 즉, 다음과 같이 표현할 수 있다.
  $S = {HH, HT, TH, TT}$
  $X(HH) = 2, X(HT) = 1, X(TH) = 1, X(TT) = 0$
  이 확률변수(확률함수)는 H가 몇번 등장하는지를 기준으로 한다고 하자.
  $P[X = 1] = P[{HT, TH}] = {2 \above 1pt 4} = {1 \above 1pt 2}$
  $P[X \leq 1] = P[{HT, TH, TT}] = {3 \above 1pt 4}$
  
  

연속확률변수(Continuous Random Variables)

• 누적분포함수(cumulative distribution function, CDF): $F(x) = P[X \in (\infty, x)]$
• 누적분포함수 $F(x)$를 가진 확률변수 $x$에 대해서 다음을 만족하는 함수 $f(x)$가 존재한다면 X를 연속확률변수라고 부르고 $f(x)$를 $X$의 확률밀도함수(probability density function, PDF)라고 부른다.
  $F(x) = \int_{- \infty}^{x} f(t)dt$
• 따라서 $F(x)$를 미분하면 $f(x)$가 되고, $f(x)$를 적분하면 $F(x)$가 된다.
• 확률변수를 명확히 하기 위해 subscript로 어떤 확률변수를 사용하는지 $F_X(x), f_X(x)$로 쓰기도 한다.
• 혼란이 없을 경우 함수 $f_X(x)$대신 소문자 p를 써서 $p_X(x), p_x(x), p(x)$를 사용하기도 한다.
• $p(x) \geq 0, \int_{- \infty}^{\infty} p(x) = 1$ 즉, 누적분포함수 $F(x)$를 미분하여 구한 도함수를 확률밀도함수 $f(x), p(x)$라고 한다!
  

확률변수의 성질(The Rules of Probability)

여기서 나오는 $p(x)$들은 모두 밀도함수라고 보면 된다.

• 덧셈법칙(sum rule): $p(X) = \sum_{Y}p(X,Y)$
• 곱셈법칙(product rule): p(X,Y) = p(X|Y)p(Y) = p(Y|X)p(X)
• 베이즈 확률(Baeys): $p(Y|X) = {p(X|Y)p(Y)} \above 1pt \sum_{Y}p(X|Y)p(Y)$
  $posterior = {likelihood * prior} \above 1pt normalization$
  - posterior: 사후확률 - likelihood: 가능도(우도) - prior: 사전확률 - normalization: Y와는 상관없는 상수. X의 경계확률(marginal) $p(X)$
  

확률변수의 함수(Functions of Random Variables)

확률변수(확률함수) $X$의 함수 $Y = f(X)$도 확률변수이다(함수의 함수). 예를 들어 확률변수 $X$가 주(week)의 수로 표현되었다고 할 때 일(day)의 수로 표현된 새로운 확률변수를 정의할 수 있다.
$Y = 7X$
$P[14 \leq Y \leq 21] = P[2 \leq X \leq 3]$
확률변수 $X$의 함수 $Y = f(X)$와 역함수 $w(Y) = X$가 주어졌을 때 다음이 성립한다.
$p_y(y) = p_x(x)|{dx \above 1pt dy}|$
우리가 원하는 것은, 새로운 확률변수 Y의 밀도함수이다. 이 밀도함수를 어떻게 계산할 것인가? 우리가 알고있는 것은 $x$에 관한 밀도함수이다. $y$의 밀도함수는 $x$의 밀도함수에 $|{dx \above 1pt dy}|$값을 곱해준 것이다.

조금 더 복잡한 경우를 보자. 하나의 확률변수가 있는 것이 아니고, $x$, $y$가 $k$개의 확률변수들의 벡터가 있다.
$k$차원의 확률변수 벡터 $x = (x_1, …, x_k)$가 주어졌을 때, $k$개의 $x$에 관한 함수들 $y_i = g_i(x) for i = 1, …, k$는 새로운 확률변수벡터 $y = (y_1, …, y_k)$를 정의한다. 간략하게 $y = g(x)$로 나타낼 수 있다.
만약 $y = g(x)$가 일대일(one-to-one)변환인 경우 ($x = w(y)$로 유일한 해를 가질 때), $y$의 결합확률밀도함수(joint pdf)는
$p_y(y_1, …, y_k) = p_x(x_1, …, x_k)|J|$

우리가 원하는 것은 새로운 확률변수의 벡터 $y$에 대해서 그것의 확률밀도함수를 원하는 것이다. 그리고 이것은 단일변수가 아니라 $k$개의 확률변수에 대한 결합확률밀도함수를 구하고자 하는 것인데, 이것을 구하는 방법은 $x$의 결합확률밀도함수에 $|J|$를 곱하는 것이다. $|J|$는 선형대수시간에 배운 determinent(행렬식)의 값에 절대값을 씌운 것이다. 야코비안(자코비안)이라고 부른다. $\partial$은 편미분을 한 것이다.
아무리 복잡한 함수라도 이런 행렬식만 구할 수 있으면, 새로 주어진 확률변수에 대해서 밀도함수를 구할 수 있다. 이는 매우 유용하고 강력한 결과이다.

예제

$p_{x_1,x_2}(x_1, x_2) = e^{-(x_1+x_2)}, x_1 > 0, x_2 > 0$라고 하자.
$y_1 = x_1, y_2 = x_1 + x_2$에 의해서 정의되는 $y$의 pdf(확률밀도함수)는?
벡터이기 때문에 y가 볼드 폰트로 표기된다.(앞서 귀찮아서 포스팅할때 일일히 볼드 표시를 하지 않았는데, $y_i$의 형태로 subscript) 즉 $y_1, y_2$의 결합확률을 구하고 싶은 것이다. 첫번째로 해야할 것은 야코비안을 구하는 것이다.
$y(x, w) = w_0 + w_1x + w_2x^2 + … + w_Mx^M = \sum_{j=0}^{M}w_jx_j$

Inverse CDF Technique

확률변수 $X$가 CDF $F_X(x)$를 가진다고 하자. 연속확률분포함수 $U ~ UNIF(0,1)$의 함수로 정의되는 다음 확률변수 $Y$를 생각해보자.
$Y = F^{-1}_X(U)$

• UNIF는 uniform distribution(연속균등분포)를 말한다. 여기서는 0부터 1까지 모두 1로만 분포되어 있다고 가정한 것.
• 누적분포함수 CDF를 가지는 확률변수 X에 대해서 샘플링을 하고싶은데, 좀 막막하다.
• 이때 uniform distribution을 가지는 확률변수 U를 통해서 또다른 확률변수 Y를 정의한 다음, 그 Y로부터 샘플링을 할 수 있다는 것이다.
• 왜 그렇게 되는지는 다음과 같이 간단하게 증명할 수 있다.
  확률변수 $Y$는 확률변수 $X$와 동일한 분포를 따르게 된다.
  $F_Y(y) = P[Y \leq y]$ : CDF의 정의
  $= P[F^{-1}_X(U)\leq y]$ : 위에서 정의한대로 $Y$를 치환.
  $= P[U \leq F_X(y)]$ : 부등식을 이와 같이 다시 표현 가능.
  $= F_X(y)$ : 확률변수 $U$가 우항의 값보다 작을 확률을 계산하면 되는데, 이 값은 $UNIF(0,1)$을 따르는 확률변수 $U$의 정의에 따라서 $F_X(y)$이 된다.
• $UNIF(0,1)$을 따르는 확률변수 $U$의 정의 : $P[U \leq u] = u$
  위의 증명에 따라, 확률변수 X와 Y가 결국 같은 분포를 따름을 알 수 있다.
  이걸 이제 실제로는 어떻게 사용하느냐?
  
  

X에 대해 CDF가 주어져 있다. $F(X)$
그럼 먼저 계산해야하는 것은 $F$의 역함수를 계산하는 것이다.
$F(X)^{-1}$이 계산될 수 있으면, $U$로부터 샘플링을 하여 여러 샘플값들을 만들어 그 값을 $F(X)^{-1}$에 집어 넣으면 된다. 즉 $U -> F(X)^{-1}(u)$
이 값들이 결국 X의 분포를 따르게 된다.

• 반경이 $r$인 원 안에 랜덤하게 점들을 찍는 프로그램? 앞서 배운 Inverse CDF Technique을 통해 이를 해결할 수 있다.
  임의의 점이 주어져 있다고 했을 때, 그 점과 원의 중심 사이의 거리를 $d$라고 하자.
  그리고 그 각도를 $\theta$라고 하자.
  $\theta$값과 $d$값의 분포를 구하면 된다.
  문제는 이게 어떤 분포일 것이냐 인데…
  $\theta$의 경우 랜덤한 점이 있을 때, $0 \leq \theta \leq 2\pi$의 값 까지 그 안에서 랜덤하게 생성을 하면 된다.
  그렇다면 $d$는? 이 $d$값이 어떤 분포를 따르는지가 가장 핵심적인 질문이다.
  $d$의 PDF를 바로 구하는 것은 힘들다. 따라서 CDF를 먼저 고려하는 것이 문제를 쉽게 풀 수 있다. (CDF를 미분하면 PDF이므로)
  CDF를 먼저 생각해보자. $F(d)$
  이는 어떤 랜덤한 점을 찍었을 때 그 점의 원점으로부터의 거리가 $d$보다 작을 확률이다.
  실제 코드로 구현하면 다음과 같다.
  ```python import turtle import math import random

wn = turtle.Screen() turtle.tracer(8,0) alex = turtle.Turtle() alex.hideturtle() r=200 for i in range(5000): u = random.random() d = r(u**0.5) # d = u * r #잘못된 경우! u를 루트를 씌우지 않고 그냥 uniform하게 샘플링했을 경우. theta = random.random()360 x = d * math.cos(math.radians(theta)) y = d * math.sin(math.radians(theta)) alex.penup() alex.setposition(x, y) alex.dot() turtle.update() wn.mainloop() ``` 점 하나를 생성하기 위해서 $d$를 올바른 확률밀도함수에 따라 샘플링하고, $theta$를 올바른 범위의 값 안에서 랜덤하게 샘플링한다.
d = u * r 로 할 경우, 원의 중심에 점들이 몰려서 찍히게 된다.

기댓값(Expectations)

• 기댓값 : 확률분포 $p(x)$하에서 함수 $f(x)$의 평균값
• 이산확률분포(discrete distribution): $E[f] = \sum_{x}p(x)f(x)$
• 연속확률분포(continous distribution): $E[f] = \int p(x)f(x) dx $
• 확률분포로부터 $N$개의 샘플을 추출해서 기댓값을 근사할 수 있다.
  $E[f] \approx {1 \above 1pt N} \sum_{N}^{n=1}f(x_n)$
• 여러개 변수들의 함수 $E_x[f(x,y)] = \sum_{x}f(x,y)p(x)$ y에 대한 함수임을 상기할 것
  $E_{x,y}[f(x,y)] = \sum_{y}\sum_{x}f(x,y)p(x,y)$
• 조건부 기댓값(conditional expectation) $E[f|y] = \sum_{x}f(x)p(x|y)$
  
  

분산(variance), 공분산(covatiance)

• $f(x)$의 분산(variance): $f(x)$의 값들이 기댓값 $E[f]$으로부터 흩어져 있는 정도

확률변수에 대한 분산과 공분산이 아닌 확률변수의 함수에 대한 분산과 공분산이다.
X, y가 아닌 x만 주어져 있을때도 계산 가능

빈도주의 대 베이지안

• 빈도주의 : 반복가능한 사건들의 빈도수에 기반
• 베이지안 : 불확실성을 정량적으로 표현

빈도주의는 구해진 파라미터의 불확실성을 부트스트랩 방법을 써서 구할 수 있다.
부트스트랩이란? : 데이터를 가지고 여러번 샘플링을 한다. 뽑았던 샘플을 다시 넣고 중복을 허용하여 N개를 뽑았을 때 그것을 D1이라고 하고,.. 이과정을 반복해 여러 데이터셋을 만들고, 각각에대해 추정자를 통해 w값을 구한다. 이 값의 변화들을 보고 파라미터에 대한 에러 바 를 만든다. 이를 통해 불확실성을 표현할 수 있다.

정규분포

단일변수 x를 위한 가우시안 분포

정규분포 : 정규화

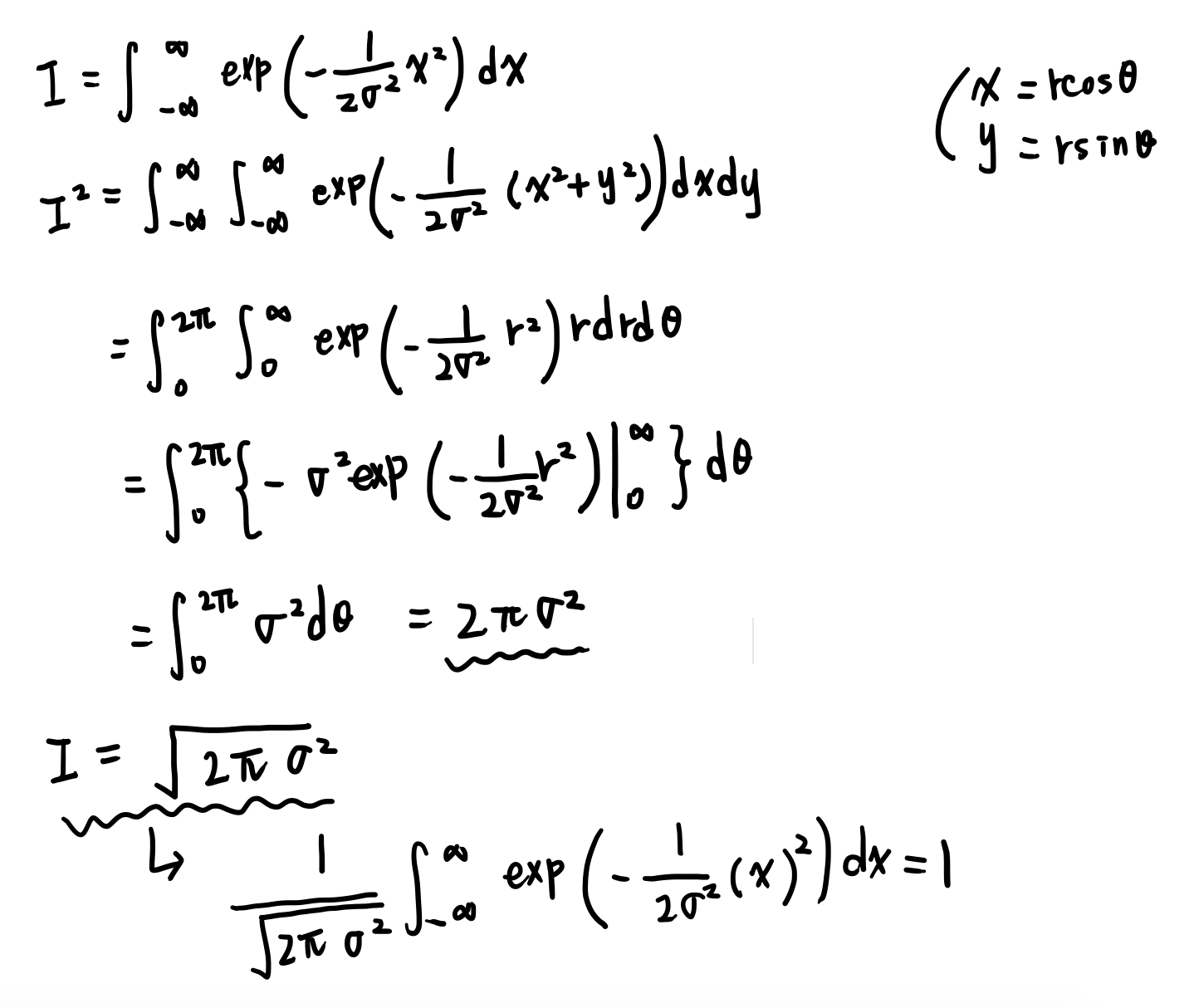
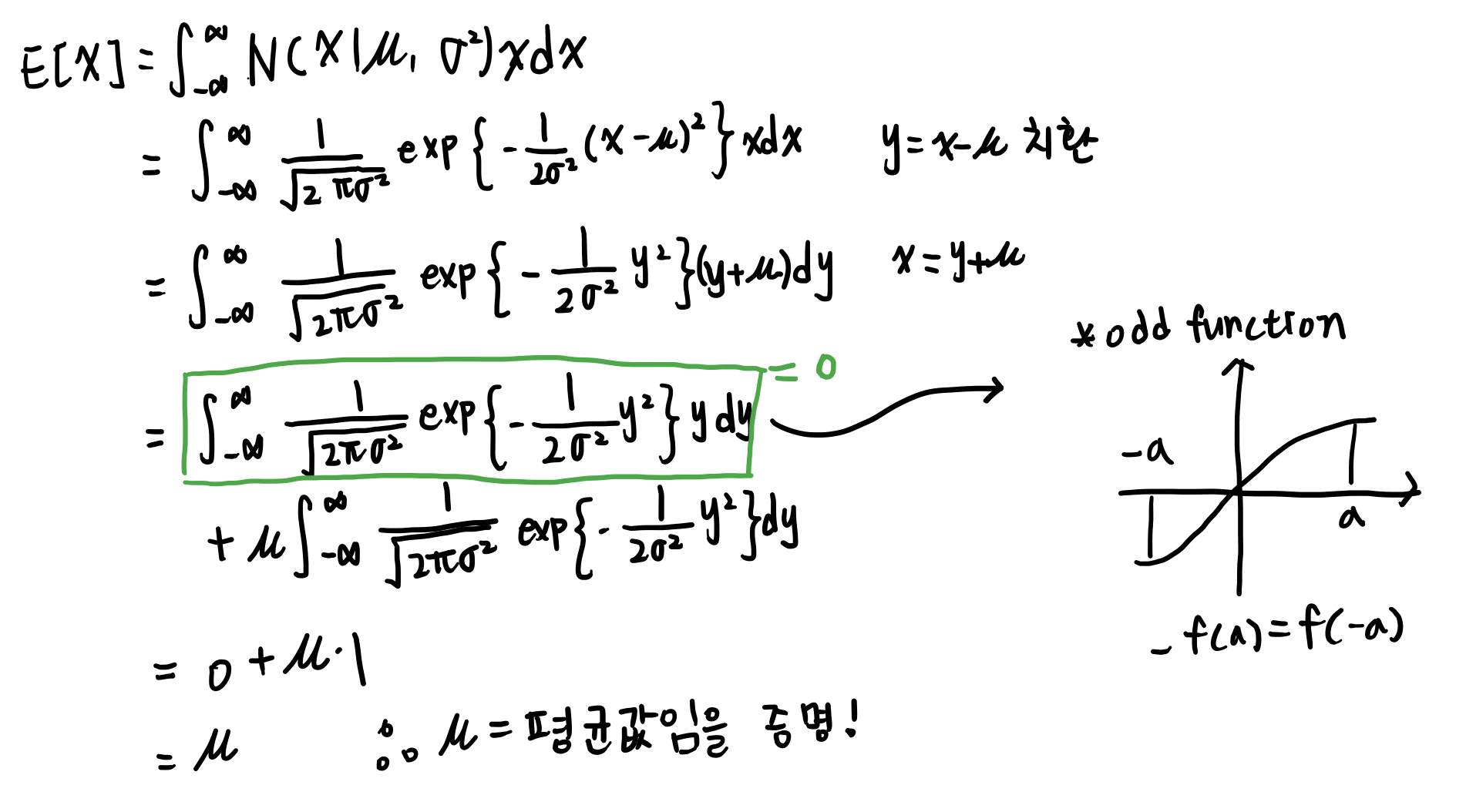
뮤=평균값
여기서 하려고하는건 함수의 형태가 가우시안 밀도 함수 형태로 주어졌을때 뮤와 시그마는 파라미터로 주어질 때 결과적으로 뮤가 그 확률변수의 기대값이 된다는 것을 보이려는 것이다. 시그마 또한 파라미터로 주어질 때 결과적으로 시그마가 분산값이 된다는것을 보일 것이다.
따라서 뮤와 시그마제곱이 평균과 분산이 됨을 보일 것이다.
Odd function : f(a)와 f(-a)값의 부호가 다르다. 적분을 하면 0이 된다.
정규분포의 기댓값은 뮤이다.

정규분포 : 분산

상수에 대해 변수로 미분을 하면 0이된다. 이 사실을 사용해서 분산값을 유도해보자. 마지막결과를 분산에 대해 풀면 시그마제곱이 나온다. 정규분포의 분산은 시그마제곱임을 증명했다.

정규분포 : 최대우도해

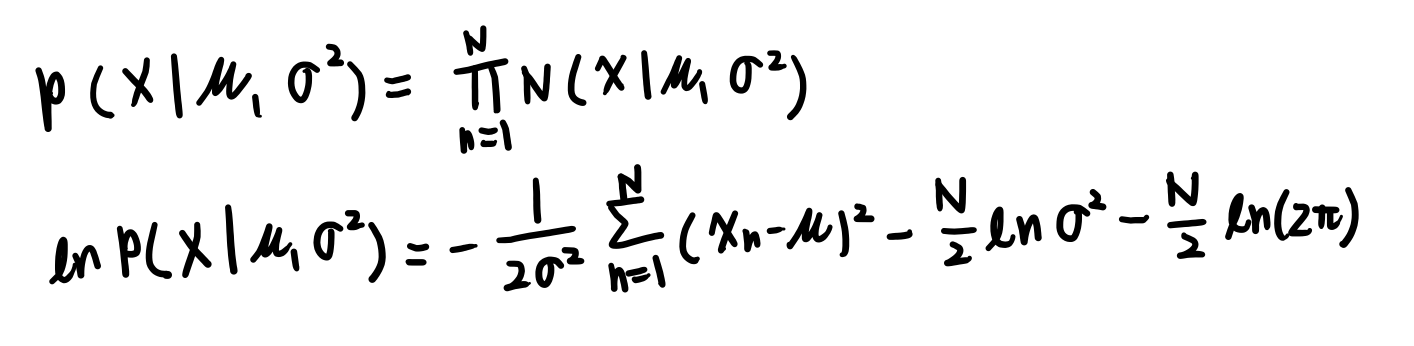
독립적인 두 확률의 값은 각각의 확률 값을 곱한 것이다 라는 것의 증명임. 증명이라기보단 정의 로그를 씌우면 좀더 다루기 쉬운 형태가 된다.

정규분포 : 최대우도해

도출된 식을 0으로 두고 뮤에 대해서 풀면 마지막 식과 같이 된다.
ML은 Maximum likelihood의 약자이다.
즉 likelihood function을 최대화 시키는 값이다.
평균을 구하려면 값들을 더해서 그 수로 나누는 당연한 것을 이렇게 수학적으로 생각한 것이다.

완전한 베이지안 곡선근사

완전한 베이지안 방법은 w의 분포로부터 확률의 기본법칙만을 사용해서 t의 예측분포를 유도한다.

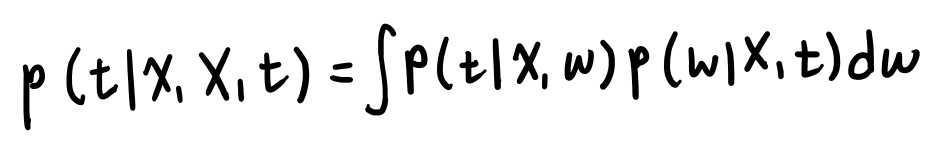
완전한 베이지안을 통해 모델링을 하게되면 값이 하나가 나오는게 아니다. 확률분포가 나오게 되는 것이다.