[Deep Learning: 신경망의 기초]신경망 기초
다층 퍼셉트론
- 인공신경망
- 기계학습 역사에서 가장 오래된 기계 학습 모델
- 퍼셉트론 -> 다층 퍼셉트론 -> 깊은 인공신경망
- 퍼셉트론 -> 다층 퍼셉트론 -> 깊은 인공신경망
- 기계학습 역사에서 가장 오래된 기계 학습 모델
신경망 기초
- 사람의 뉴런 : 두뇌의 가장 작은 정보처리 단위
- 구조
- 세포체는 간단한 연산
- 수상돌기는 신호 수신
- 축삭은 처리 결과를 전송
- 구조
- 뉴런을 모방한 것이 퍼셉트론이다.
신경망의 종류
- 인공신경망은 다양한 모델이 존재함
- 전방 신경망과 순환 신경망(순환 방향의 차이 : 단방향/순환)
- 얕은 신경망과 깊은 신경망(은닉층의 차이)
- 결정론 신경망과 확률론적 신경망 비교
- 결정론 신경망 : 모델의 매개변수와 조건에 의해 출력이 완전히 결정되는 신경망
- 확률론적 신경망 : 고유의 임의성을 가지고 매개변수와 조건이 같더라도 다른 출력을 가지는 신경망
퍼셉트론
- 구조: node(절), weight(가중치), layer(층)과 같은 새로운 개념의 구조 도입
- 제시된 퍼셉트론 구조의 학습 알고리즘을 제안
- 원시적 신경망이지만, 깊은 인공신경망을 포함한 현대 인공신경망의 토대
- 깊은 인공신경망은 퍼셉트론의 병렬 배치를 순차적으로 구조로 결합함
- 현대 인공신경망의 중요한 구성 요소가 됨
구조
- 퍼셉트론의 구조
- 입력
- i번째 노드는 특징 벡터 $x$의 요소 $x_i$를 담당
- 항상 1이 입력되는 편향(bias) 노드 포함
- 입력과 출력 사이에 연산하는 구조를 가짐
- i번째 입력 노드와 출력 노드를 연결하는 edge는 가중치 $w_i$를 가짐
- 퍼셉트론은 단일 층 구조라고 간주함
- 출력
- 한 개의 노드에 의해 수치(+1 혹은 -1) 출력
- 한 개의 노드에 의해 수치(+1 혹은 -1) 출력
- 입력
동작
- 퍼셉트론의 동작
- 선형 연산 -> 비선형 연산
- 선형 : 입력(특징)값과 가중치를 곱하고 모두 더해 $s$를 구함
- 비선형 : 활성함수 $\tau$를 적용
- 활성함수 $\tau$로 계단 함수(step function)를 사용 -> 출력 $y=+1$ 또는 $y=-1$
- 수식
- $y = \tau(s)$
- $s = w_0 + \sum_{i=1}^{d}w_ix_i$
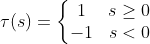
- 선형 연산 -> 비선형 연산
- 행렬 표기
- $s = w^Tx + w_0$
- 편향 항(bias term = $w_0$와 그 뒤에 곱해져 있던 1)을 벡터에 추가하면, $s = w^Tx$(즉 0점으로 옮기는 작업이다)
- 퍼셉트론의 동작을 이 식으로 표현할 수 있음.
- $y = \tau(w^Tx)$
- $y = \tau(w^Tx)$
위의 결과를 기하학적으로 설명하면, 결정 직선은 특징 공간을 +1과 -1의 두 부분공간으로 이분할하는 분류기 역할.
임계값을 구분하는 비선형함수인 활성함수를 0점에서 비교하도록 만들어주는 것이다.
- d차원 공간으로 일반화하면
- 2차원 : 결정 직선, 3차원 : 결정 평면, 4차원 이상 : 결정 초평면
- 2차원 : 결정 직선, 3차원 : 결정 평면, 4차원 이상 : 결정 초평면
학습
- 퍼셉트론의 학습
- 지금까지 학습을 마친 퍼셉트론의 동작을 설명
- 가중치 벡터, 즉 파라미터 $w$가 어떤 값을 가져야 옳게 분류할까?
- 실제값과 예측값이 일치하도록 손실함수를 낮추면서 올바른 가중치 벡터를 찾는 것이 학습이다.
- 일반적인 분류기의 학습과정
- 단계1 : 과업 정의와 분류 과정의 수학적 정의(가설 설정)
- 단계2 : 해당 분류기의 목적함수 $J(\Theta)$ 정의
- 단계3 : $J(\Theta)$를 최소화하는 $\Theta$를 찾기 위한 최적화 방법 수행
- 목적함수 정의 (단계1 + 단계2)
- 퍼셉트론(가설 혹은 모델 설정)의 매개변수를 $w$라 표기하면, 매개변수 집합은 $\Theta = {w}$ 표기
- 목적함수를 $J(\Theta)$ 또는 $J(w)$로 표기(손실함수)
- 퍼셉트론 목적함수의 상세 조건
- $J(w) \geq 0$이다.
- $w$가 최적이면, 즉 모든 샘플을 맞히면 $J(w) = 0$이다.(주어진 데이터가 완전분할된다고 가정했을 때)
- 틀리는 샘플이 많은 $w$일수록 $J(w)$는 큰 값을 가진다.
- 목적함수 상세 설계
- $J(w) = \sum_{x_k\in Y}-y_k(w^Tx_k)$
- $Y$는 $w$가 틀리는 샘플의 집합
- 조건1 만족 : 임의의 샘플 $x_k$가 $Y$에 속한다면, 퍼셉트론의 예측 값 $w^Tx_k$와 실제 값 $y_k$는 부호가 다름 -> $-y_k(w^Tx_k)$는 항상 양수를 가짐(오분류되면 마이너스 값이 나오므로 거기에 또 마이너스를 붙이면 양수가 됨. 즉 예측값과 실제값의 부호가 서로 다름. 예측 -1, 실제 +1인 경우 서로 곱하고 -를 붙이면 양수!)
- 조건2 만족 : 결국 $Y$가 클수록(틀린 샘플이 많을수록), $J(w)$는 큰 값을 가짐
- 조건3 만족 : $Y$가 공집합일 때(즉, 퍼셉트론이 모든 샘플을 맞출 때), $J(w) = 0$임
- 경사 하강법(단계3)
- 최소 $J(\Theta)$ 기울기를 이용하여 반복 탐색하여 극값을 찾음
- 손실함수(목적함수)의 미분의 값이 최소화 되도록 해야함.
- 경사도 계산
- 일반화된 가중치 갱신 규칙 $\Theta = \Theta - \rho g$를 적용하려면 경사도 $g$가 필요. rho, 즉 $\rho$는 learning rate(학습률), $\Theta$는 가중치, $g$는 그래디언트.
- 목적함수(손실함수)를 편미분하면,
- ${\partial J(w) \above 1pt \partial w_i} = \sum_{x_k\in Y}-y_kx_{ki}$
- 편미분 결과를 대입하면,
- 델타 규칙 : $w_i = w_i + \rho \sum_{x_k\in Y}y_kx_{ki}$
- 델타 규칙은 퍼셉트론의 학습 방법
-
학습률(learning rate)는 한번 업데이트할 때마다 얼마나 움직일지 결정한다. 너무 작아서도 안되고, 너무 커서도 안된다.
- 퍼셉트론 학습 알고리즘(확률론적 형태)
- 샘플 순서를 섞고, 틀린 샘플이 발생하면 즉시 갱신
- 입력 : 훈련집합 $X$와 $Y$, 학습률 $\rho$
- 출력 : 최적 가중치 $\widehat{w}$

- 행렬 표기
- 델타규칙을 하나의 w에서 벡터 w에 대하 확장하면 다음과 같다.
- $w = w + \rho y_jx_j$
- 델타규칙을 하나의 w에서 벡터 w에 대하 확장하면 다음과 같다.
- 선형분리 불가능한 경우에는 무한 반복됨
