[인공지능 수학 - 미적분]4강 : 행렬연산과 선형조합
행렬연산과 선형조합
행렬 표기법과 관련 용어
행렬(matrix)은 직사각형 구조에 숫자들을 담아 놓은 구조이다. 각 숫자들의 행렬의 요소(entry)라 부른다.
다음은 3개의 행(row)와 2개의 열(column)으로 이루어진 3*2 행렬이다.
$
\begin{bmatrix}
3 & 1\cr
1 & -2\cr
2 & -4
\end{bmatrix}
$
다음과 같이 하나의 행 혹은 하나의 열을 가지는 특별한 행렬을 각각 행벡터(row vector), 열벡터(column vector)라 한다.
$
\begin{bmatrix}
2 & 1 & 0 -3
\end{bmatrix}
$
$
\begin{bmatrix}
1\cr
3
\end{bmatrix}
$
극단적으로 1*1 행렬의 경우, 스칼라(scalar)라고 한다.
$
\begin{bmatrix}
4
\end{bmatrix}
$
$m*n$ 행렬은 다음과 같이 $m * n$개의 숫자가 직사각형 구조에 채워진 형태로 표기할 수 있다. $ A = \begin{bmatrix} a_{11} & a_{12} & \ldots & a_{1n} \cr a_{21} & a_{22} & \ldots & a_{2n} \cr \vdots & \vdots & \ddots & \vdots \cr a_{m1} & a_{m2} & \ldots & a_{mn} \cr \end{bmatrix} $
주요 표기법
- 행렬 A의 각 (i, j)요소는 $a_{ij}$로 나타낸다.
- 행렬 A를 간략히 표기할 때는 $A = [a_{ij}]$로 나타낸다.
- 행렬 A의 크기가 중요할 경우는 $A = [a_{ij}]_{m*n}$로 나타낸다.
Transpose Matrix(전치행렬)
$m * n$행렬 A에 대한 transpose matrix(전치행렬) $A^T$는 A의 행을 열로, A의 열을 행으로 가지는 $n*m$ 행렬이다. 즉, $A^T_{ij} = A_{ji}$를 만족한다.
$
A = \begin{bmatrix}
1 & 2\cr
3 & 4\cr
5 & 6
\end{bmatrix}
$
$
A^T = \begin{bmatrix}
1 & 3 & 5\cr
2 & 4 & 6
\end{bmatrix}
$
벡터 표기법
벡터는 아래의 x와 같이 볼드체 소문자로 표기한다. 선형대수에서는 보통 벡터라고 하면 열벡터를 기본으로 한다.
$
X = \begin{bmatrix}
x_1\cr
x_2\cr
…\cr
x_n
\end{bmatrix}
$
주요 표기법
- 벡터라고 하면 일반적으로 열벡터(column vector)를 말한다.
- n-벡터는 n개의 스칼라(scalar)로 구성된 열벡터를 말한다.
Zero Matrices(영행렬)
행렬의 모든 요소가 0이면, 해당 행렬을 영행렬(zero matrix)라 하고 O로 표기한다.
$A + O = O + A = A$
숫자 세계에서의 0과 같은 취급을 하며, 교환법칙 등 또한 성립한다.
영행렬은 숫자의 0과 같은 존재로 행렬합에 대한 항등원 역할을 한다.
행렬의 합 : 두 행렬 A와 B는 행과 열의 개수가 모두 같을 때 성립하며, 각 (i, j)-요소의 합으로 정의된다.
$n*n$ 행렬 : Square Matrix(정방행렬)
행과 열의 개수가 모두 n인 정사각형(square)모양의 행렬을 n차 square matrix(정방행렬)이라 한다.
$
A = \begin{bmatrix}
a_{11} & a_{12} & \ldots & a_{1n} \cr
a_{21} & a_{22} & \ldots & a_{2n} \cr
\vdots & \vdots & \ddots & \vdots \cr
a_{n1} & a_{n2} & \ldots & a_{nn} \cr
\end{bmatrix}
$
특히, $a_{ii} (i = 1, 2, …, n)$를 행렬 $A_n$의 main diagonal(주대각선)이라 한다.
Identity Matrices(항등행렬)
주대각선(main diagonal)이 1이고 나머지 요소는 모두 0인 n차 정방행렬(square matrix)을 항등행렬(identify matrix)이라 한다.
$
I_n = \begin{bmatrix}
1 & 0 & \ldots & 0 \cr
0 & 1 & \ldots & 0 \cr
\vdots & \vdots & \ddots & \vdots \cr
0 & 0 & \ldots & 1 \cr
\end{bmatrix}
$
항등행렬은 숫자의 1과 같은 존재로 행렬곱에 대한 항등원 역할을 한다.
[중요] 행렬의 곱
$m * r$ 행렬 $A=[a_{ij}]$ 와 $r * n$행렬 $B=[b_{ij}]$가 있을 때, 두 행렬의 곱 AB는 $m * n$ 행렬 $C=[c_{ij}]$를 정의한다.
여기서 두 행렬의 곱 AB로 정의된 행렬 C의 각 (i, j)-요소는 다음과 같이 정의된다.(A의 행 * B의 열) 즉 내적의 값을 나열한 것이다.
$c_{ij} = a_{i1} + a_{i2}b_{2j} + … + a_{ir}b_{rj}$
행렬의 곱에서 반드시 숙지해야할 사항
- 행렬 C의 각 요소 $c_{ij}$는 ‘곱의 왼쪽 행렬 A의 i번째 행벡터’와 ‘곱의 오른쪽 행렬 B의 j번째 열벡터’의 내적(inner product)이다.
- 따라서, 두 행렬의 곱 AB에 대해 A의 열 개수와 B의 행 개수는 일치해야 한다.
- 일반적으로 AB != BA이다. 왜냐하면 행과 열을 뽑아오는 방법이 다르기 때문이다. 교환법칙이 성립하지 않는다.
- 행렬의 곱은 병렬처리(parallel processing)로 가속할 수 있다. 즉 독립적으로 계산될 수 있다.
스칼라, 벡터, 행렬, 그리고 텐서: 계층적 구조 이해하기
스칼라 -> 벡터 -> 행렬
스칼라는 숫자 하나로 구성되어 있다.
$7$
이 스칼라를 벡터로 표현하면 아래와 같이 1개의 구성요소로 이루어진 1-벡터가 된다.
$[7]$
이 스칼라를 행렬로 표현하면 아래와 같이 1개의 구성요소로 이루어진 1*1 행렬이 된다.
$[7_{11}]$
벡터 -> 행렬
벡터는 여러 숫자가 일열로 늘어선 구조이다.
$
\begin{bmatrix}
1\cr
2\cr
3\cr
4
\end{bmatrix}
$
이 벡터를 행렬로 표현하면 여러 모양의 행렬로 표현할 수 있다.
- 4*1 행렬
- 2*2 행렬
- 2*2 행렬의 전치행렬
- 1*4 행렬 표현하고자 하는 행렬의 모양은 응용문제에 따라 결정!
행렬 -> 벡터
행렬은 사각형 구조에 여러 숫자가 행과 열로 늘어선 구조이다.
$
\begin{bmatrix}
1 & 2 & 3\cr
4 & 5 & 6
\end{bmatrix}_{2*3}
$
이 행렬은 다음과 같이 6-벡터로 표현할 수 있다.
$
\begin{bmatrix}
1\cr
2\cr
3\cr
4\cr
5\cr
6
\end{bmatrix}
$
$
\begin{bmatrix}
1\cr
4\cr
2\cr
5\cr
3\cr
6
\end{bmatrix}
$
행렬을 벡터로 변환할 때, 행부터 혹은 열부터 읽을 것인지는 응용문제에 따라 결정!
텐서
텐서(tensor)는 스칼라, 벡터, 행렬을 아우르는 개념이다. 숫자가 늘어설 수 있는 방향이 k개면 k-텐서로 부른다.
- 0-텐서 : 스칼라 (숫자가 늘어설 수 있는 방향이 없다)
- 1-텐서 : 벡터 (숫자가 늘어설 수 있는 방향이 한 방향이다)
- 2-텐서 : 행렬 (숫자가 늘어설 수 있는 방향이 두 방향이다)
- 4-텐서 : 동영상
만일 아래의 T의 각 요소 $P_{ij}$가 벡터라면, T는 3-텐서로 볼 수 있다.
$ T = \begin{bmatrix} P_{11} & P_{12} & P_{13} & P_{14} \cr P_{21} & P_{22} & P_{23} & P_{24} \cr P_{31} & P_{32} & P_{33} & P_{34} \cr P_{41} & P_{42} & P_{43} & P_{44} \cr \end{bmatrix} $
3-텐서의 대표적인 예는 컬러영상이다. $P_{ij}$가 3-벡터이면 RGB영상을, 4-벡터이면 RGBA영상을 나타낸다.
분할행렬(Partitioned Matrix) : 선형대수에서 가장 중요한 개념!!
행렬을 조각(partition) 단위로 분할하여 생각해도 무방하다. 이런 관점에서 본다면, 행렬은 부분행렬(submatrix)로 이루어진 직사각형 구조로 확장해서 생각할 수 있다. 이렇게 행렬을 구조적으로 보는 방법을 분할행렬(partitioned matrix)또는 블록행렬(block matrix)이라 한다.
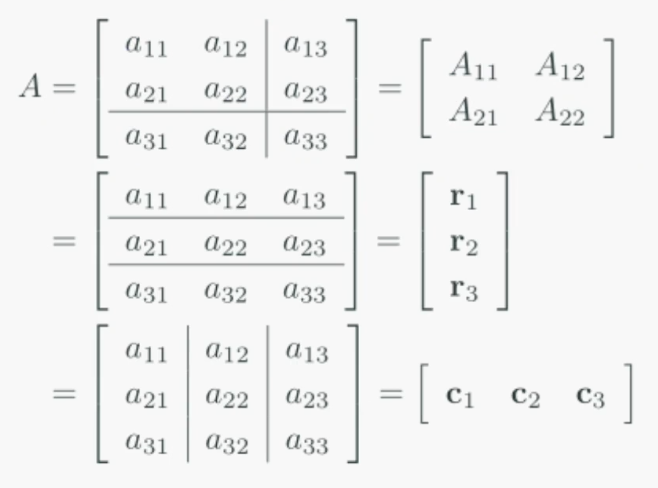
이렇게 행렬을 조각조각 분할(행벡터 단위로, 열벡터 단위로, …)해서 계산해도 무방하다!!
행렬은 행벡터의 모임 / 열벡터의 모임으로 나타낼 수 있다!
보통 열벡터의 모임으로 많이 쓰인다.
분할행렬로 행렬의 곱 이해하기
두 행렬의 곱 AB = C를 아래와 같이 matrix-column vector products로 볼 수 있다.
$
AB = A *
\begin{bmatrix}
b_1 & b_2 & \ldots & b_n
\end{bmatrix}
=
\begin{bmatrix}
Ab_1 & Ab_2 & \ldots & Ab_n
\end{bmatrix}
= C
$
예를 들면, $A_{23}B_{32} = C_{22}$을 다음과 같이 구조적으로 해석할 수 있다.
$
\begin{bmatrix}
\alpha & \alpha & \alpha\cr
\alpha & \alpha & \alpha
\end{bmatrix}
$
*
$
\begin{bmatrix}
\alpha & \alpha\cr
\alpha & \alpha\cr
\alpha & \alpha
\end{bmatrix}
$
=
$
\begin{bmatrix}
\alpha & \alpha\cr
\alpha & \alpha
\end{bmatrix}
$
$
A*\begin{bmatrix}
b_1 & b_2
\end{bmatrix}
$
=
$
\begin{bmatrix}
Ab_1 & Ab_2
\end{bmatrix}
$
두 행렬의 곱 AB = C를 아래와 같이 row vector-matrix products로도 볼 수 있다.
$
AB = \begin{bmatrix}
a_1\cr
a_2\cr
\dots\cr
a_m
\end{bmatrix}
$
*B =
$
\begin{bmatrix}
a_1B\cr
a_2B\cr
\dots\cr
a_mB
\end{bmatrix}
= C
$
예를 들면, $A_{23}B_{32} = C_{22}$을 다음과 같이 구조적으로 해석할 수 있다.
$
\begin{bmatrix}
\alpha & \alpha & \alpha\cr
\alpha & \alpha & \alpha
\end{bmatrix}
$
*
$
\begin{bmatrix}
\alpha & \alpha\cr
\alpha & \alpha\cr
\alpha & \alpha
\end{bmatrix}
$
=
$
\begin{bmatrix}
\alpha & \alpha\cr
\alpha & \alpha
\end{bmatrix}
$
$
\begin{bmatrix}
a_1\cr
a_2
\end{bmatrix}
*B =
\begin{bmatrix}
a_1B\cr
a_2B
\end{bmatrix}
$
선형조합(Linear Combination): Ax는 A의 열벡터에 대한 선형조합
행렬을 구조적으로 보기
행렬은 열벡터의 리스트이다.
$
A = \begin{bmatrix}
a_{11} & a_{12} & \ldots & a_{1n} \cr
a_{21} & a_{22} & \ldots & a_{2n} \cr
\vdots & \vdots & \ddots & \vdots \cr
a_{m1} & a_{m2} & \ldots & a_{mn} \cr
\end{bmatrix}
=
\begin{bmatrix}
a_1 & a_2 & \dots & a_n
\end{bmatrix}
$
여기서 $a_i$는 행렬 A의 i-번째 열벡터이다. 특히 각 열벡터는 m-벡터이기 때문에, $m*n$행렬은 m-벡터가 n개 있다고 해석!
행렬@벡터 연산을 구조적으로 보기
Ax는 행렬 A가 가지고 있는 열벡터의 선형조합이다.
$
Ax = \begin{bmatrix}
a_{11} & a_{12} & \ldots & a_{1n} \cr
a_{21} & a_{22} & \ldots & a_{2n} \cr
\vdots & \vdots & \ddots & \vdots \cr
a_{m1} & a_{m2} & \ldots & a_{mn} \cr
\end{bmatrix}
*
\begin{bmatrix}
x_1\cr
x_2\cr
\dots\cr
x_n
\end{bmatrix}
$
=
$
\begin{bmatrix}
a_1 & a_2 & \dots & a_n
\end{bmatrix}
$
*
$
\begin{bmatrix}
x_1\cr
x_2\cr
\dots\cr
x_n
\end{bmatrix}
$
$
= x_1a_1 + x_2a_2 + \dots + x_na_n
$
선형대수에서는 이처럼 벡터들에 대한 가중치 합을 선형조합(linear combination)이라 부른다.
Ax의 결과는 행렬 A가 가지고 있는 열벡터의 선형조합으로만 한계가 지어진다.
[중요] 선형시스템 Ax = b를 선형조합 관점에서 바라보기
$ Ax = \begin{bmatrix} 1 & 3 & 2 \cr 1 & 2 & -3 \cr 2 & 1 & -2 \cr \end{bmatrix} * \begin{bmatrix} x_1\cr x_2\cr x_3\cr \end{bmatrix} = \begin{bmatrix} 1\cr -9\cr -3\cr \end{bmatrix} $
(좌항)선형조합으로 해석한 Ax
$x_1$
*
$
\begin{bmatrix}
-1\cr
1\cr
2\cr
\end{bmatrix}+
$
$x_2$
*
$
\begin{bmatrix}
3\cr
2\cr
1\cr
\end{bmatrix}+
$
$x_3$
*
$
\begin{bmatrix}
2\cr
-3\cr
-2\cr
\end{bmatrix}
$
(우항) b
$
\begin{bmatrix}
1\cr
-9\cr
-3\cr
\end{bmatrix}
$
(정리) 선형시스템 Ax=b를 선형조합 관점에서 바라보기
행렬 A의 열벡터를 가중치합으로 선형조합할 때 벡터 b를 만들 수 있는 가중치 조합이 존재한다면, 선형시스템 Ax=b의 해는 존재한다. 그 해는 가중치 $x_i$들로 구성된 x이다.
Column Space(열공간)
행렬 A의 열벡터들에 대한 가능한 모든 선형조합의 결과를 모아 집합으로 구성할 수 있을 것이다. 이를 집합을 column space(열공간)이라 하고 다음과 같이 표기한다.
$col(A)$
Consistent Linear System
선형시스템 Ax=b가 해를 가지면 다음을 만족한다.
$b \in col(A)$
Consistent Linear System
선형시스템 Ax=b가 r가 없으면 다음을 만족한다.
$b \notin col(A)$
