[인공지능 수학 - 미적분]5강 : 좌표계변환

좌표계 변환(Change of Basis): 좌표계::좌표값 = 행렬::벡터

$Ax = Ib$
$A$ : 좌표계
$x$ : 좌표값
$I$ : 표준좌표계
$b$ : 좌표값

벡터의 표현

벡터는 크기와 방향을 가진 물리량으로 다음과 같이 표현할 수 있다.
벡터의 물리적 표현(좌표계 없는 표현)
벡터 v를 화살표로 표현한다.

• v의 크기 : 화살표의 길이
• v의 방향 : 화살표의 방향

벡터의 수학적 표현(좌표계 있는 표현)
벡터 v를 화살표로 표현한다.
좌표계를 도입한 후, 벡터의 시작점을 원점에 맞추고 끝점의 위치(x,y) 를 벡터 v의 수학적 표현으로 정의한다.

• v의 크기 : 화살표의 길이를 계산
• v의 방향 : 화살표의 방향을 벡터로 표현

좌표계(Coordinate System)

좌표를 쓴다는건 좌표계가 있다는 것이다. 다음과 같이 2-벡터 v가 주어졌다고 하자. 이 벡터는 xy-평면 상에서는 원점 (0, 0)에서 시작하여 (a, b)에서 끝나는 벡터를 의미한다. v는 다음과 같이 해석될 수 있다.
$ v = \begin{bmatrix} a\cr b\cr \end{bmatrix} = \begin{bmatrix} 1 & 0\cr 0 & 1\cr \end{bmatrix} \begin{bmatrix} a\cr b\cr \end{bmatrix} = a \begin{bmatrix} 1\cr 0\cr \end{bmatrix} +b \begin{bmatrix} 0\cr 1\cr \end{bmatrix} $
v=(a,b)에 곱해준 것은 항등행렬이다. 항등행렬의 열벡터에 a와 b를 각각 곱해 선형조합의 형태로 만들 수 있다. a[1 0]은 x축(x축으로 한칸 전진, x축으로 내린 수선의 발)을, b[0 1]은 y축(y축으로 한칸 전진, y축으로 내린 수선의 발)을 의미한다.
결과적으로 항등행렬 자체가 직교좌표계를 표현한다고 정리할 수 있다. 그리고 각각의 좌표값은 일종의 각 축에 내린 수선의 발과 의미를 같이한다.

• $a\begin{bmatrix} 1\cr 0\cr \end{bmatrix}$ : x-축으로 내린 수선의 발, 즉 x-축의 단위로 a번 전진함.
• $b\begin{bmatrix} 0\cr 1\cr \end{bmatrix}$ : y-축으로 내린 수선의 발, 즉 y-축의 단위로 b번 전진함.
• xy-좌표계 : $b\begin{bmatrix} 1 & 0\cr 0 & 1\cr \end{bmatrix}$

항등행렬을 좌표계로 볼 수 있다면, 다른 행렬 또한 좌표계로 볼 수 있다.
만일 두 벡터 v1과 v2를 이용해 새롭게 좌표계를 만든다면 v의 좌표값은 무엇일까? 새로운 좌표계를 만든다는 말은 어떤 벡터 v에 도착하기 까지의 과정을 오롯이 v1과 v2를 몇번 사용하여 도착했는지로 표현한다는 의미이다.
예를 들어, v1과 v2를 이용해 만든 새로운 좌표계에서 v의 좌표값은 (4,3)이라 해야한다. 왜냐하면
$4v_1 + 3v_2 = v$
이기 때문이다.

지금까지의 전체과정을 행렬로 표현하면 아래와 같다.
$ \begin{bmatrix} v_1 & v_2\cr \end{bmatrix} \begin{bmatrix} 4\cr 3\cr \end{bmatrix} = \begin{bmatrix} v\cr \end{bmatrix} = \begin{bmatrix} a\cr b\cr \end{bmatrix} $
$v_1$을 4번 써서 전진하고, $v_2$를 3번 써서 전진했을 때 $v$지점에 도착했다. $[v]$의 앞에는 사실 항등행렬이 숨겨져 있다. 즉, 좌표계(표준좌표계)가 숨겨져 있다.
$ \begin{bmatrix} v_1 & v_2\cr \end{bmatrix} \begin{bmatrix} 4\cr 3\cr \end{bmatrix} = \begin{bmatrix} e_1 & e_2\cr \end{bmatrix} = \begin{bmatrix} a\cr b\cr \end{bmatrix} $
위 식의 (좌항)과 (우항)이 표현하는 바는 다음과 같다.

• (좌항) : $v_1$과 $v_2$를 기저(basis)로 가지는 좌표계(coordinate system)에서는 동일한 벡터 $v$의 좌표값은 (4, 3)이다.
• (우항) : $e_1$과 $e_2$를 기저(basis)로 가지는 표준좌표계(standard coordinate system)에서 벡터 v의 좌표값은 (a, b)이다.

좌표계 변환(Change of Basis)

선형시스템(linear system)문제를 좌표계 변환으로 바라보면 다음과 같다.
$Ax = b$
A는 좌표계이다. x는 좌표계에 대한 좌표값이다. b는 좌표값인데 그 앞에 표준좌표계(I, 항등행렬)이 숨어져 있다.

• (좌항) : A의 열벡터들을 기저(basis)로 가지는 좌표계에서는 동일 벡터의 좌표값은 x이다.
• (우항) : 표준좌표계(standard cordinate system)에서 어떤 벡터의 좌표값은 b이다. 즉, 동일한 지점에 대해서 서로 다른 이름이 존재할 수 있다. 왜냐하면 좌표계가 달라지기 때문이다.
  $\begin{bmatrix} 1 & -1\cr 2 & 2\cr \end{bmatrix} \begin{bmatrix} 2\cr 1\cr \end{bmatrix} = \begin{bmatrix} 1\cr 6\cr \end{bmatrix} $

역행렬을 이용해 선형시스템의 해를 구하는 문제 역시 좌표계 변환으로 바라볼 수 있다.
$x = A^{-1}b$

• (좌항) : 표준좌표계(standard cordinate system)에서 어떤 벡터의 좌표값은 x이다.
• (좌항) : $A^{-1}$의 열벡터들을 기저(basis)로 가지는 좌표계에서는 동일 벡터의 좌표값은 b이다. $Ax = b$ b를 기준으로 하여 b앞에 표준좌표계(항등행렬)이 붙음.
  $ \begin{bmatrix} 1 & -1\cr 2 & 2\cr \end{bmatrix} \begin{bmatrix} 2\cr 1\cr \end{bmatrix} = \begin{bmatrix} 1\cr 6\cr \end{bmatrix} $ => $A^-1b = x$
  역행렬을 하면 x를 기준으로 하여 x앞에 표준좌표계(항등행렬)이 붙음. x를 기준으로 봤을때, 첫번째 축을 한칸 전진한다는 것은 [1/2, -1/2]만큼 전진한다는 것이고 두번째 축을 한칸 전진한다는 것은 [1/4, 1/4]만큼 전진한다는 것이다. 아, 왼쪽항이 그만큼 전진한다면 x가 [2,1]이라고 부르는 것은 b에게 있어 [1.6]인 것이다.
  $ \begin{bmatrix} 1/2 & 1/4\cr -1/2 & 1/4\cr \end{bmatrix} \begin{bmatrix} 1\cr 6\cr \end{bmatrix} = \begin{bmatrix} 2\cr 1\cr \end{bmatrix} $
  동일한 문제이지만 바라보는 관점에 따라 다르게 표현될 수 있다. 선형시스템은 좌표계 변환이라고 해석할 수 있다.

정리

행렬은 좌표계이고, 벡터는 좌표값이다. 임의의 v는 다양한 좌표계에서 표현될 수 있다.
$v$(표준좌표계에서 표현된 v) = $A$(좌표계 A) $\begin{bmatrix} v \end{bmatrix} _A
$
$[v]_A$를 구했다는 것은 A라는 행렬이 정의하는 좌표계의 각각의 basis들을 몇번 써서 v라는 지점에 도착할 수 있는지를 구한 것이다.
결론적으로, 좌표계를 행렬로 구성하고, 그 옆에 곱해져있는 벡터를 해당 좌표계에서의 좌표값이라고 할 수 있다.
이와 같은 수식을 통해 A 또는 B 좌표계 기준으로 표준좌표계를 쓸 수 있다.

예제 1 : 좌표계 변환(Change of Basis)

2-벡터 벡터 v가 표준좌표계에서 (2,3)으로 표현된다고 하자. 벡터(3,1)과 (1,-2)를 기저벡터로 가지는 새로운 좌표계를 도입했을 때, 해당 벡터 v는 어떤 좌표값을 가질까?

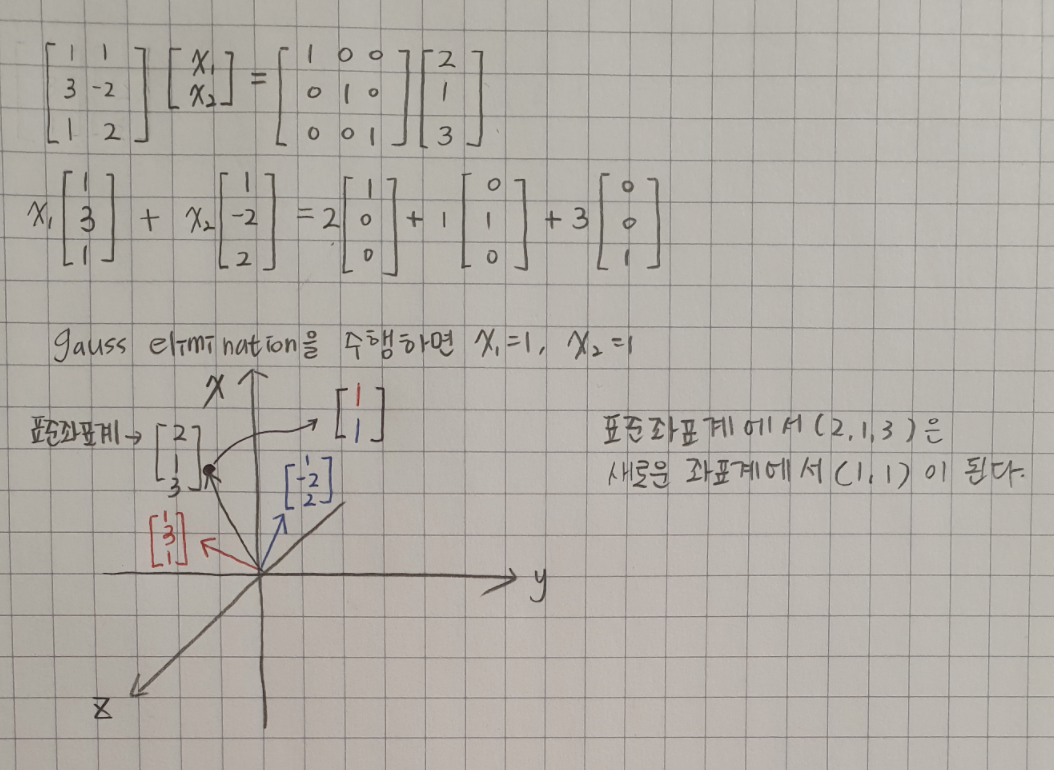
예제 2 : 좌표계 변환(Change of Basis)

3-벡터 벡터 v가 표준좌표계에서 (2,1,3)으로 표현된다고 하자. 벡터(1,3,1)과 (1,-2,2)를 기저벡터로 가지는 새로운 좌표계를 도입했을 때, 해당 벡터 v는 어떤 좌표값을 가질까?