[인공지능 수학 - 확률과 확률분포]13강 : 확률분포
확률 변수(random variable)
- 랜덤한 실험 결과에 의존하는 실수(흰공, 검은공 이런거 안됨!)
- 즉 표본 공간의 부분 집합에 대응하는 실수
- 주사위 2개를 던지는 실험
- 주사위 숫자의 합 : 하나의 확률 변수
- 주사위 숫자의 차 : 하나의 확률 변수
- 두 주사위 숫자 중 같거나 큰 수 : 하나의 확률 변수
- 동전 10개를 던지는 실험
- 동전의 앞면의 수
- 첫번째 앞면이 나올 때까지 던진 횟수
- 보통 표본 공간에서 실수로 대응되는 함수로 정의
-
보통 X나 Y같은 대문자로 표시
- 이산확률변수
- discrete random variable
- 확률변수가 취할 수 있는 모든 수 값들을 하나씩 셀 수 있는 경우(정수, 유리수)
- 주사위, 동전과 관련된 예
- 연속확률변수
- continuous random variable
- 셀 수 없는 경우
- 어느 학교에서 랜덤하게 선택된 남학생의 키(나올 수 있는 값이 무수히 많으면서, 일일히 셀 수 없다) 이산확률변수인 경우 값이 정수인 경우가 많고, 연속확률변수인 경우 값이 실수인 경우가 많다.
확률 분포
- Probability Distribution
- 확률변수가 가질 수 있는 값에 대해 확률을 대응시켜주는 관계
- 예)
- 어떤 확률 변수 X가 가질 수 있는 값 : 0, 1, 3, 8
- 각 값이 나올 확률
- $P(X = 0) = 0.2$
- $P(X = 1) = 0.1$
- $P(X = 3) = 0.5$
- $P(X = 8) = 0.2$
- 확률분포의 표현 : 매우 다양함
- 표, 그래프, 함수, …
- 주사위 2개를 던지는 실험
- 확률 변수 X : 주사위 숫자의 합
- X가 가질 수 있는 값
- 2, 3, …, 12
- $P(X = 12) = 1/36$
- X가 가질 수 있는 값
- 확률 변수 Y : 주사위 숫자의 차
- Y가 가질 수 있는 값
- 0, 1, 2, …, 5
- $P(X = 5) = 2/36 = 1/18$
- Y가 가질 수 있는 값
- 확률 변수 X : 주사위 숫자의 합
- 주사위 2개를 던지는 실험
- 확률 변수 X : 주사위 숫자의 합
- 주사위를 던질 때마다 X의 값이 달라질 수 있음
- n번 실험하면, n개의 숫자가 나옴
- 이 n개의 숫자의 평균과 분산을 계산할 수 있음
- 확률 변수 X도 평균과 분산을 가짐
- 이 평균과 분산을 모집단의 평균과 분산이라고 할 수 있음
이산확률변수
- 이산확률변수의 확률분포
- 보통 함수로 주어짐
- 확률변수 X가 x라는 값을 가질 확률
- P(X = x) = f(x)
- 확률질량함수
- 예)
- 확률변수 X가 가질 수 있는 값 : 0, 2, 5
- P(X = x) = f(x) = (x+1)/10
- P(X=0) = 0.1
- P(X=2) = 0.3
- P(X=5) = 0.6
- 이산확률변수의 평균
- 기대값(expected value)라고도 함
- $E(X) = \Sigma_x xP(X = x) = \Sigma_x xf(x)$
- $E(X) = 0 * 0.1 + 2 * 0.3 + 5 * 0.6 = 3.6$
- 위 계산이 왜 타당한지 예를 들어서 살펴보자.
- 예를 들어 100,000번의 실험을 했다면
- 0이 대략 10,000번 나옴
- 2이 대략 30,000번 나옴
- 5가 대략 60,000번 나옴
- 따라서 평균은
- ${(0 * 10000 + 2* 30000 + 5 * 60000) \above 1pt 100000} = 0 * 0.1 + 2 * 0.3 + 5 * 0.6 = 3.6$
- 몇번을 하더라도 결국 3.6에 수렴하게 된다. 이 값을(이산확률변수의 평균) 기대값이라고 한다.
- 이산확률변수의 분산
- $(X - \mu)^2$의 평균
- $\sigma^2 = E[(X - \mu)^2] = \Sigma_x(x = \mu)^2 P(X = x)$
- 0,2,5 그리고 평균 3.6을 넣어서 계산해보면 3.24가 나온다.
- $Var(X)$라고도 함
- 이산확률변수의 표준편차
- 분산의 양의 제곱근. 분산에 루트를 씌우면 된다. 표준편차의 제곱은 분산!
- $\sqrt \sigma^2 = \sigma$
- $SD(X)라고도 함$
- 확률변수 X의 분산 : 간편식
- $\sigma^2 = E(X^2) - {E(X)}^2$
결합확률 분포
- join probability distribution
- 두 개 이상의 확률 변수가 동시에 취하는 값들에 대해 확률을 대응시켜주는 관계
- 확률변수 X
- 한 학생이 가지는 휴대폰의 수
- 확률변수 Y
- 한 학생이 가지는 노트북의 수
- $\sigma^2 = {1 \above 1pt N}\sum_{i=1}^{N}(x_i - \mu)^2$
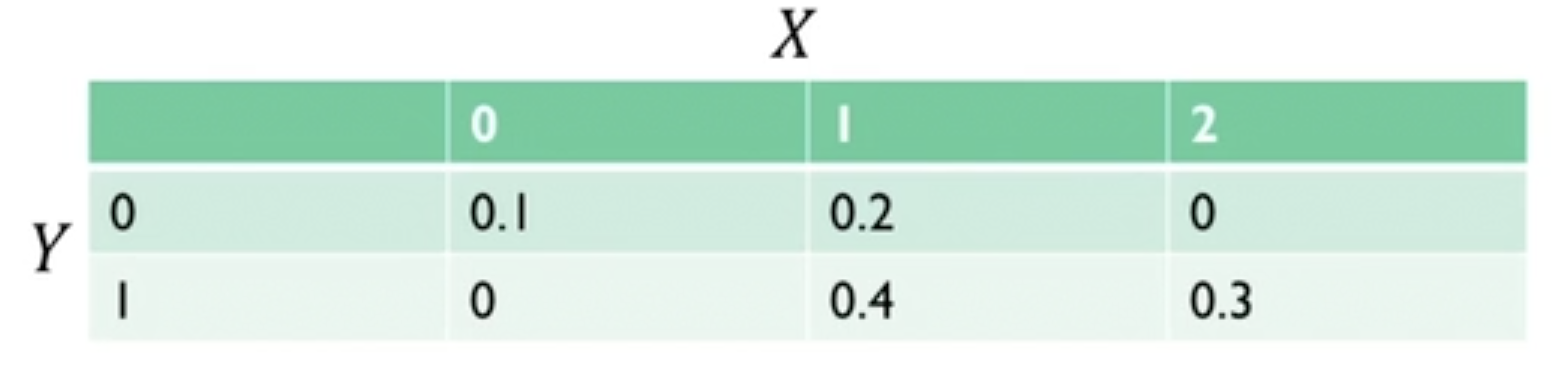
- 결합확률분포를 통해 각 확률변수의 확률 분포를 도출할 수 있음. 이를 주변확률분포(marginal probability distribution)이라고 함.
- X의 확률분포(X의 각 칼럼들을 더함)

- Y의 확률분포(Y의 각 행들을 더함)

공분산
- 확률변수 사이의 관계를 알아볼 수 있다.
- 고등학교 1학년 학생들
- 확률변수 X : 키
- 확률변수 Y : 몸무게
- 확률변수 Z : 수학성적
- $(X - \mu_X)(Y - \mu_Y)$ : 양일 가능성이 높음(일반적으로, 키가 크면 몸무게도 크기 때문)
- $(X - \mu_X)(Z - \mu_Z)$ : 양과 음이 될 가능성이 반반(키와 수학성적은 관계가 없음)
- $(X - \mu_X)(Y - \mu_Y)$와 $(X - \mu_X)(Z - \mu_Z)$
- 이와 같은 수식 각각이 확률변수. 랜덤한 실험 결과에 의해 나오는 실수이다.
- 따라서 평균과 분산을 구할 수 있음
- Covariance
- 확률변수 X와 Y의 공분산
- $(X - \mu_X)(Y - \mu_Y)$의 평균
- $Cov(X, Y) = E[(X - \mu_X)(Y - \mu_Y)] = E(XY) - \mu_x \mu_y = E[XY] - E[X]E[Y]$
- 공분산을 통해 X, Y값이 서로 관련이 있는지 알 수 있다. 관련이 있다면 양의값/음의값으로 나온다. 관련이 없다면 어쩔땐 양의값, 어쩔땐 음의값이 나와서 결과적으로 0에 가까운 값이 나온다.
-
즉, 공분산이 0에 가까울수록 두 값이 서로 관련이 없다.
- 위의 예시에서 대학생의 핸드폰과 노트북 소지에 대해 공분산을 구해보면 다음과 같다.
- $E[XY] = 1 * 1 * 0.4 + 2 * 1 * 0.3 = 1.0$
- $E[X] = 1 * 0.6 + 2 * 0.3 = 1.2$
- $E[Y] = 1 * 0.7 = 0.7$
- $Cov(X, Y) = E[XY] - E[X]E[Y] = 1.0 - 1.2 * 0.7 = 0.16$
상관계수
- 공분산은 각 확률 변수의 절대적인 크기에 영향을 받음
- 단위에 의한 영향을 없앨 필요
- $\rho = Corr(X, Y) = {Cov(X, Y) \above 1pt \sigma_X \sigma_Y}$
- 상관계수를 이용하면 X, Y의 절대적인 크기에 상관없이 비례관계를 볼 수 있다.
